درسته.
آقا گرفتم چی شد. خود نویسنده هم همینو میگه:
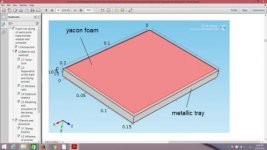
Well, so that you can understand my answers, please take a look at Figure 1: L (lenght), W (width) and tau (thickness) are the dimensions of the computational domain (yacon foam tray). Being L the lenght of the tray, it means that everything that happens in the right side, happens also in the left side of the tray. Hence, for economy of computational time, we don't have to solve the entire domain, otherwise we would be solving the same mathematical problem twice, understand? In summary, L/2 defines the half lenght of the foam tray (left and right sides of it).
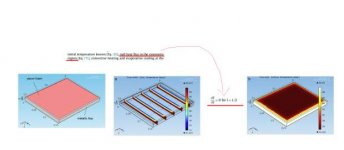
The boundary condition to be used for the bottom part of the tray can be a simple conduction equation, such as q=k x deltaT (and then you would use the conductivity k of the tray's material). Basically, the tray is being heated by the drying air (there's a deltaT between air and tray) and this heat flux (q) is transmitted to the food.
فقط این تیکه دوم حرفشون گفتن میشه برای کف سینی ، یه معادله هدایت ساده در نظر گرفت ، یعنی این معادله رو در نظر بگیرید:
q=k x deltaT
اخه در کامسول یه هیت فلاکس داریم که نشان دهنده ی کنوکسیون هست و فرمولشم در قسمت هیت فلاکس موجوده به این صورت:
q=h deltaT
برای هدایت حرارتی (همین فرمول اولی) مگه ما شرط مرزی داریم؟ولی من این فرمول رو در کامسول ندیدم:
q=k x deltaT