You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
·▪•تاپیک بیان و رسیدگی به سوالات ریاضی و آمار●•▪·
- شروع کننده موضوع Kruger
- تاریخ شروع
درود.ابتدا سوال 2 رو میگم که حفظش کردم.!z2 رو در مزدوج مخرج ضرب کن تا از حالت گویا خارج بشه بعد مزدوجشو به دست بیار و در آخر در z1 ضرب کن .سوال سوم ابتدا از طرفین LN بگیر بعد مشتق بگیر با اینکار سینوس به پشت LN میاد و به یک مشتق حاصلضرب تبدیل میشه و با یک سری عملیات ریاضی ساده حل میشه.سوال 4 رو دقیق نمیدونم.سوال یک هم ابتدا آرگومان رو به دست بیار بعدمقدار عددی عدد مختلط رو حساب کن که میشه رادیکال2 که اینجا با ریشه سومش کار داری ریشه سوم رادیکال 2 رو باید در e به توان i در پرانتز x+180کل عبارت تقسیم بر n ضرب کنی.که x همون آرگومانه و مقدار n رو از صفر تا 2 باید سه مرتبه یعنی یکبار صفر بعد 1 و در آخر 2 قرار بدی تا ریشه های معادله به دست بیاد.با عذر پوزش اگه کمی گنگه.بیانش برام سخت بود.سلام دوستان. راه حل این مسائل رو کی می دونه؟
جواب سوال چهارم:
یکی از راههای بدست آوردن وارون یک تابع؛ابتدامحاسبهyبرحسبxمیباشد بطوریکه درنهایت به جای هرچه xداریم قرارمیدهیمyوبجای هر چه yکه درفرمول بدست آمده داریم قرارمیدهیمx.
خب پس برای بدست آوردن وارون تابع :

سعی میکنیم ابتداx را برحسب yبدست آوریم؛ پس بطورمعادل قرارمیدهیم:

حال صورت ومخرج کسرفوق را در
 ضرب میکنیم بدست می آید:
ضرب میکنیم بدست می آید:
 که ازاینجا یه معادله درجه دو بدست میاد که با حل آن داریم:
که ازاینجا یه معادله درجه دو بدست میاد که با حل آن داریم:
 بنابراین داریم:
بنابراین داریم:

حال همانطورکه گفته شد جای xوy راعوض میکنیم جواب نهایی بدست میاد:

تمام.
یکی از راههای بدست آوردن وارون یک تابع؛ابتدامحاسبهyبرحسبxمیباشد بطوریکه درنهایت به جای هرچه xداریم قرارمیدهیمyوبجای هر چه yکه درفرمول بدست آمده داریم قرارمیدهیمx.
خب پس برای بدست آوردن وارون تابع :

سعی میکنیم ابتداx را برحسب yبدست آوریم؛ پس بطورمعادل قرارمیدهیم:

حال صورت ومخرج کسرفوق را در




حال همانطورکه گفته شد جای xوy راعوض میکنیم جواب نهایی بدست میاد:

تمام.

با سلام جواب سه تا سوال آخر رو بچه هل به خوبی دادن به نظرم کامله ولی در مورد سوال اول یک نگاه به لینک زیر بندازین
http://www.suitcaseofdreams.net/Roots_complex.htm
راه حل رو در مورد مساله خودتون مرحله به مرحله دنبال کنین ،البته میتونین به صورت نمایی هم حلش کنین همونطور که میبینین از تبدیل اعداد مختلط به فرم مثلثاتی و نمایی استفاده میشه و با عنیات به این نکته که دوره تناوب سینوس و کسینوس دو پی هست
برای چک کردن جواب ها سعی کنین جواب ها رو ساده کنین و به سایت http://www.wolframalpha.com/input/?i=z^3=1-i برین
موفق باشین
http://www.suitcaseofdreams.net/Roots_complex.htm
راه حل رو در مورد مساله خودتون مرحله به مرحله دنبال کنین ،البته میتونین به صورت نمایی هم حلش کنین همونطور که میبینین از تبدیل اعداد مختلط به فرم مثلثاتی و نمایی استفاده میشه و با عنیات به این نکته که دوره تناوب سینوس و کسینوس دو پی هست
برای چک کردن جواب ها سعی کنین جواب ها رو ساده کنین و به سایت http://www.wolframalpha.com/input/?i=z^3=1-i برین
موفق باشین
با سلام جواب سه تا سوال آخر رو بچه هل به خوبی دادن به نظرم کامله ولی در مورد سوال اول یک نگاه به لینک زیر بندازین
http://www.suitcaseofdreams.net/Roots_complex.htm
راه حل رو در مورد مساله خودتون مرحله به مرحله دنبال کنین ،البته میتونین به صورت نمایی هم حلش کنین همونطور که میبینین از تبدیل اعداد مختلط به فرم مثلثاتی و نمایی استفاده میشه و با عنیات به این نکته که دوره تناوب سینوس و کسینوس دو پی هست
برای چک کردن جواب ها سعی کنین جواب ها رو ساده کنین و به سایت http://www.wolframalpha.com/input/?i=z^3%3D1-i برین
موفق باشین
با تشکر از راهنمایی شما دوست عزیز. ضمنا این جزوه PDF فارسی هم در حل این مساله میتونه کارساز باشه.
پیوست ها
ببینید من راه حلشو میگم......اون عبارت داخل پرانتزو بدون این که توانش چنده رو (منظور اینه توانشو یک در نظر بگیرید) بعد به نمایش قطبی تبدیل کنید که زاویش میشه ارک تانژانت 1/2 که در ربع دوم قرا داره چون قسمت موهومیش یا همون ایگرگش منفیه بعدش چون توی ربع دوم قرار داره باید به اندازه ی پی از اون زاویه ای که بدست اوردید کم کنید تا تتا یا همون زاویه ی اصلی بدست بیاد و مقدار r میشه رادیکال 5 بعدش توی فرمول نمایش قطبی جایگذاری کنید
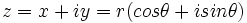
و طبق قضیه ی دموار

به راحتی به توان 4 برسونید و دوباره این بار جواب بدست اومده رو از مختصات قطبی به دکارتی تبدیل کنید....
در ضمن تنها راه درست حل این مساله همینه
نه این که بخوایم همون عبارتو از اول به توان 4 برسونیم چون که فلسفه تبدیل مختصات دکارتی به قطبی همینه که توی مختصات قطبی خیلی راحت میتونیم عملیات ضرب و تقسیمو و توان رسانی و....رو انجام بدیم...
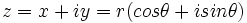

به راحتی به توان 4 برسونید و دوباره این بار جواب بدست اومده رو از مختصات قطبی به دکارتی تبدیل کنید....
نه این که بخوایم همون عبارتو از اول به توان 4 برسونیم چون که فلسفه تبدیل مختصات دکارتی به قطبی همینه که توی مختصات قطبی خیلی راحت میتونیم عملیات ضرب و تقسیمو و توان رسانی و....رو انجام بدیم...
bigbomber
کاربر فعال
تعیین ریشه های مختلط یک معادله
تعیین ریشه های مختلط یک معادله
سلام
استاد پرژه ای داده اند با عنوان " برنامه ای بنویسید برای تعیین ریشه های مختلط یک معادله ".
این پروژه مربوط به درس محاسبات عددی ( رشته ی مکانیک ) است. راستیتش من این درس را یکمی زود برداشتم و الان در قسمت ریاضیات این پروژه مشکل دارم. برنامه نویسی، زبان MATLAB مسلط هستم.
اگر لطف کنید من را راهنمایی بفرمایید، بسیار سپاس گزارم.
با تشکر.
تعیین ریشه های مختلط یک معادله
سلام
استاد پرژه ای داده اند با عنوان " برنامه ای بنویسید برای تعیین ریشه های مختلط یک معادله ".
این پروژه مربوط به درس محاسبات عددی ( رشته ی مکانیک ) است. راستیتش من این درس را یکمی زود برداشتم و الان در قسمت ریاضیات این پروژه مشکل دارم. برنامه نویسی، زبان MATLAB مسلط هستم.
اگر لطف کنید من را راهنمایی بفرمایید، بسیار سپاس گزارم.
با تشکر.
mohammadreza1001
کاربر فعال
پیوست ها
farizin
عضو جدید
خیلی راحت
مشاهده پیوست 91071
مشاهده پیوست 91071
پیوست ها
mohammadreza1001
کاربر فعال
بله.n ریشه بدست می آید که هرکدام ممکن است حقیقی یا مختلط باشند.کلا معادله درجه nام n ریشه مختلط دارد.مثلا معادله x[SUP]2[/SUP]-2x+4=0 ریشه حقیقی ندارد.اما دو ریشه مختلط دارد.ضمن تشکر از همه ی دوستان، علی الخصوص آقایان محمد و فرزین.
آقا محمد، با روشی که گفتید ریشه های مختلط هم به دست می آید؟
با تشکر.
اشکالی که ایشون گفتن وارده.من به سوال شما دقت نکردم.فکر نمی کنم برای معادلات درجه سوم و بالاتر در دامنه اعداد حقیقی روش مشخصی وجود داشته باشد.برای حل اینگونه معادلات به بررسی حالات خاص می پردازیم یا از روش های دبیرستان مثل نصف کردن و نیوتن و ... استفاده می کنیم.اما در مورد معادلات مختلط مثل معادله بالا باید بگم تو کتاب های ریاضی مهندسی که داشتم هم زیاد به این موضوعات نپرداخته بود.دوست عزیز روش شما برای یافتن ریشه های معادله Z^n=k به درد میخوره و با اون جوابهای مختلط چند جمله های ها به دست نمیاد.
مثلاً برای یافتن ریشه های معادله Z^4-2*Z^2+Z=4=0 روش شما منجر به تشکیل دو چند جمله ای مجدد میشه.
bigbomber
کاربر فعال
با تشکر.
اساتید من در نرم افزار متلب با دستور R=Roots(p) ریشه های حقیقی و مختلط معالات چند جمله ای را به دست می آورم. اما متوجه روش حل نرم افزار نمی شوم. اگر لطف کنید یک نگاهی بندازید به الگوریتم و توضیح دهید که چگونه ریشه را به دست می آورد بسیار سپاس گزارم.
آقای محمد، آیا با روش نصف کردن و یا نیتون می شود ریشه های مختلط معادلات را به دست آورد؟ اگر جواب مثبت است لطفاً کمی توضیح دهید.
با تشکر.
اساتید من در نرم افزار متلب با دستور R=Roots(p) ریشه های حقیقی و مختلط معالات چند جمله ای را به دست می آورم. اما متوجه روش حل نرم افزار نمی شوم. اگر لطف کنید یک نگاهی بندازید به الگوریتم و توضیح دهید که چگونه ریشه را به دست می آورد بسیار سپاس گزارم.
آقای محمد، آیا با روش نصف کردن و یا نیتون می شود ریشه های مختلط معادلات را به دست آورد؟ اگر جواب مثبت است لطفاً کمی توضیح دهید.
با تشکر.
Kruger
عضو جدید
کاملا موافقم تصمیم فوق العاده خوبی هست.
مثله انجمن پی سی ورد
اونجا یه اتاق ریاضی داره
یه اتاق امار و احتمال
یه اتاق حساب دیفرانسیل انتگرال
یه اتاق مثلثات
و چند اتاق دیگه
این باعث میشه پراکندگی خیلی کاهش پیدا کنه
یاعلی
تصیمیم جالب گرفتید ... من که امادگی خودمو برای رفع اشکالا اعلام میکنم
یه چیزایی بلدم از ریاضی
خیلی ممنون از حمایتتون
سلام بیزحمت فرمولای مثلات چه اصلیا چه فرعیا یه جا میخوام کسی داره؟؟

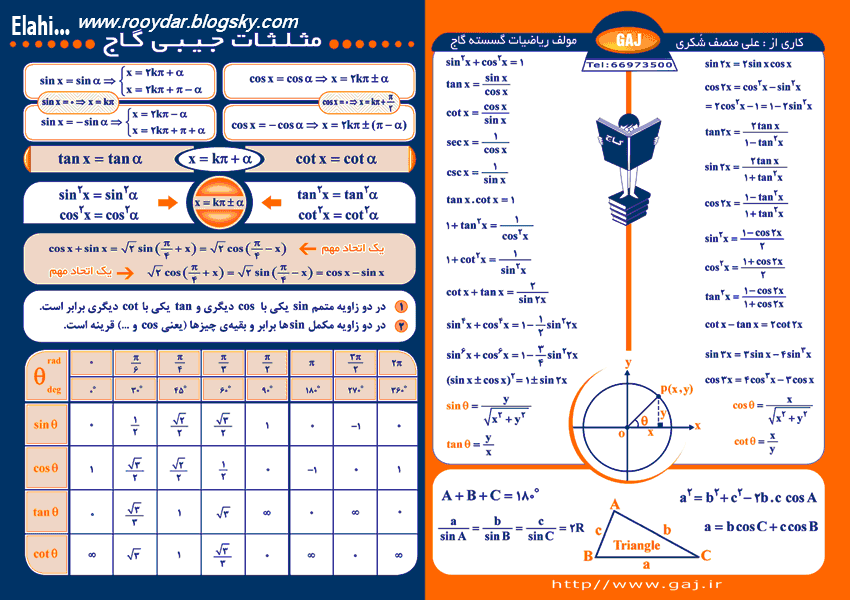
25 تا 50 یا 100 تا 125 یا ...تا ...+25سلام من یه سوال دارم ۲۵ عدد صحیح متمایز فهرست کنید که بتوان دو عدد به گونه ای از بین این ۲۵ عدد انتخاب کرد که هیچ کدام از ۲۳ عدد باقی مانده جمع و یا تفاضل این دو عدد نباشند. ممنون می شم راهنمایی کنید
Javid64
عضو جدید
سلام بر ریاضیدانان عزیز
ازونجایی که من چندین سال پیش درسهایی مثل محاسبات و آمار و کلا همه ی درسهای رشتمونو شب امتحانی پاس کردم، روش میانیابی خطی یادم رفته
حالا یه سوال داشتم
توی فهرست بهای ما بتن با مقاومت 20 مگاپاسکال را مترمکعبی 41300 تومن حساب کرده و مقاومت 25 مگاپاسکال را 44150
و گفته که قیمت مقاومت های بین 20 و 25 مگاپاسکال را با میانیابی خطی بدست آورین
حالا مقاومت طراحی من 24 مگاپاسکاله
میتونین راهنماییم کنید چجوری درونیابیش باید کنم که هیچی یادم نمیاد از جریان کار!
ازونجایی که من چندین سال پیش درسهایی مثل محاسبات و آمار و کلا همه ی درسهای رشتمونو شب امتحانی پاس کردم، روش میانیابی خطی یادم رفته
حالا یه سوال داشتم
توی فهرست بهای ما بتن با مقاومت 20 مگاپاسکال را مترمکعبی 41300 تومن حساب کرده و مقاومت 25 مگاپاسکال را 44150
و گفته که قیمت مقاومت های بین 20 و 25 مگاپاسکال را با میانیابی خطی بدست آورین
حالا مقاومت طراحی من 24 مگاپاسکاله
میتونین راهنماییم کنید چجوری درونیابیش باید کنم که هیچی یادم نمیاد از جریان کار!
*Essi*
اخراجی موقت
سلام بر ریاضیدانان عزیز
ازونجایی که من چندین سال پیش درسهایی مثل محاسبات و آمار و کلا همه ی درسهای رشتمونو شب امتحانی پاس کردم، روش میانیابی خطی یادم رفته
حالا یه سوال داشتم
توی فهرست بهای ما بتن با مقاومت 20 مگاپاسکال را مترمکعبی 41300 تومن حساب کرده و مقاومت 25 مگاپاسکال را 44150
و گفته که قیمت مقاومت های بین 20 و 25 مگاپاسکال را با میانیابی خطی بدست آورین
حالا مقاومت طراحی من 24 مگاپاسکاله
میتونین راهنماییم کنید چجوری درونیابیش باید کنم که هیچی یادم نمیاد از جریان کار!
اول باید شیب خط از دو نقطه معلومت رو به دست بیاری.
که میشه اختلاف y ها، تقسیم بر اختلاف x ها.
حالا که شیب رو به دست آوردی میدونیم چون این نقطه مجهول ما روی همین خطه پس دارای شیب یکسان هستند.
پس شیب بین دو نقطه رو که به دست آوردی برابر با شیب حاصل از یکی نقاط معلوم مثل 25 و نقطه 24 برابر قرار میدی که فقط یک مجهول داری و به دست میاد.
(هادی)
کاربر فعال تالار ریاضی ,
اول باید شیب خط از دو نقطه معلومت رو به دست بیاری.
که میشه اختلاف y ها، تقسیم بر اختلاف x ها.
حالا که شیب رو به دست آوردی میدونیم چون این نقطه مجهول ما روی همین خطه پس دارای شیب یکسان هستند.
پس شیب بین دو نقطه رو که به دست آوردی برابر با شیب حاصل از یکی نقاط معلوم مثل 25 و نقطه 24 برابر قرار میدی که فقط یک مجهول داری و به دست میاد.
سلام
به عبارت دیگه باید بگی من 20 و 25 رو دارم اما چیزی که میخوام نه اینه نه اون. بلکه به نسبت 1 به 5 به 25 نزدیک تره یعنی فاصله اون از 25 یک پنجم فاصله 20 از 25 هست. پس قیمتش هم همین جوره. فاصله اش از قیمت 25 مگاپاسکالی (44150) یک پنجم فاصله قیمت 20 مگا تا 25 مگا میشه
جواب میشه 43580.
kooshiRiman
عضو جدید
حل معادله ی root x+y =11 && rooty+x=7
حل معادله ی root x+y =11 && rooty+x=7
سلام . خیلی وقته که دنبال حل معادله :
root x+y =11 && rooty+x=7
هستم ....
من یه راهی می رم که خیلی متفاوته با راه اصلی اگه کسی روشی برا حل این معادله داره ...به من بگه ...!!!!

باتشکر...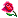
حل معادله ی root x+y =11 && rooty+x=7
سلام . خیلی وقته که دنبال حل معادله :
root x+y =11 && rooty+x=7
هستم ....
من یه راهی می رم که خیلی متفاوته با راه اصلی اگه کسی روشی برا حل این معادله داره ...به من بگه ...!!!!

باتشکر...
کتابهای فارسی تو این انجمن برای دانلود قرار نمیگیرن. بخاطر حفظ حقوق نویسنده و ناشرسلام
لطفآ کتاب ریاضیات پایه،نویسنده:لیدا فرخو،انتشارات دانشگاه پیام نور
رو در انجمن آپلود بفرمایید.با آرزوی موفقیت هر چه بیشتر
اگه این کتاب که شما میخواهید واقعا تو نت باشه میتونید با یه سرچ تو گوگل بدست بیاریدش.
سلام. یه سوال داشتم مربوط میشه به ریاضیات دبیرستان! خالم دبیر ریاضی هستش و یه فرمول گفته به شاگرداش. اونا هم سوال پیچش کردن که چرا این فرمول؟!! حالا سوال اینه که تو بحث جایگشت وقتی مثلا بخوایم چند نفر رو دور یه میز بشونیم میگیم (n-1)فاکتوریل حالت داره!. در حالیکه میدونیم جایگشت مثلا تو یه صف (!) میشه nفاکتوریل. (من الان 2ساله که با دنیای ریاضی خداحافظی کردم اینا الان اصلا یادم نیست )
)
 )
)



