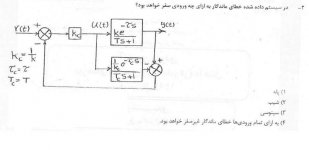
اریاز دو فرمول معروف برای محاسبه خطای حالت ماندگار داره یکی اینکه تابع تبدیل حلقه بسته را بدست بیاری و از طریق اون خروجی را حساب کنی و بعد بگی خطا میشه حد s*(خروجی-ورودی) وقتی s به سمت صفر میل میکنه. یا فرمول دوم اینکه حد s ضرب در ورودی تقسیم بر (1+حلقه باز) حالا سوال من اینه:
برای چه سیستم هایی نمیتونیم خطا را از دو فرمول بالا حساب کنیم. به عبارت دیگه معادله مشخصه یا تابع تبدیل حلقه باز یا تابع تبدیل حلقه بسته چه ویزگی داشته باشند تا دو فرمول بالا در مورد انها صادق نباشد.
و سوال دوم این که در مورد چنین سیستم هایی خطای حالت ماندگار را چگونه محاسبه کنیم؟
اول اینکه خطا برای سیستم پایدار تعریف میشود یعنی اگر سیستم ناپایدار باشد مقدار خروجی کراندار نخواهد بود و خروجی ورودی را اصلا دنبال نمی کند . پس اساسا تعریف خطا مفهوم نخواهد داشت
به همین علت است همواره برای تعینن خطا حوسمان باید به پایداری سیستم باشد
خطا معمولا از فرمول sR/1+GH بدست میاید که این فرمول همان روش تعین k می باشد (k متناسب با ورودی تعینن میشود که ثابت های خطای موقعیت ، سرعت و شتاب می باشد)
در اینجا باید دقت کنیم که تابع تبدیل حلقه باز تعیین کننده خطا می باشد.
بدست اوردن خطا بی نهایت در حوزه زمان همان بدست اوردن خطا در حوزه لاپلاس و میل دادن ان به سمت صفر است.
این بحث ، که کی میشه از قضیه مقدار نهایی در حوزه لاپلاس استفاده شود باید شرایط خاصی بر مسئله حکم فرما باشد
فرض کنید مقدار f(t ) در بی نهایت را میخواهیم حساب کنیم می توانیم معادل ان را در حوزه لاپلاس شبیه سازی کنیم
f(s) را فرض میکنیم داریم حال میتوانیم یک اس در ان ضرب کرده و ان را به سمت صفر میل میدهیم
فقط باید دقت کنی وقتی اس را در اف اس ضرب کردی باید دارای شرایط زیر باشد تا بتوان از این قضیه مقدار نهایی استفاده کرد وگرنه این امکان پذیر نخواهد بود
1- اس اف اس باید پایدار مجانبی باشد یعنی هیچ گونه قطبی سمت راست خود و روی محور موهومی نداشته باشد قطب در مبدا مشکلی در قضیه بوجود نخواهد اورد
حال اگر این شرایط برقرار باشد براحتی میتوانیم مقدار نهایی را حساب کنیم.
همین تعاریف را میتوانیم برای تابع تبدیل حلقه باز و نحوه بدست اوردن ثابت های خطا بکار بست.
در بعضی سیستم ها نیز خطا را حاصل تفریق ورودی منهای خروجی در حوزه زمان میدانند . معمولا وقتی که صحبتی از این قضیه نشود حالت اول مد نظر است
ولی در کل باید احتیاط کرد و حواسمان به تعریف دوم نیز باشد.




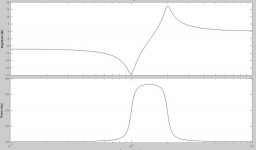
 )
)