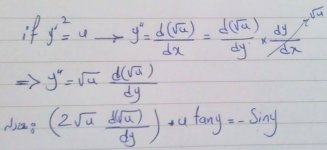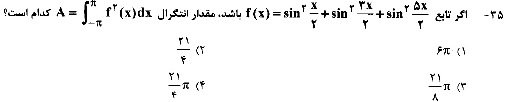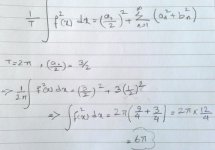تاپیک رفع اشکال درس ریاضیات کنکور کارشناسی ارشد

[hts1369]

سلام بر دوستان عزیز
چاکرم
دوستان لطف میکنند در مورد این سوال راهنمایی کنند.
تو کلید زده گزینه اول ولی من راه حلی به ذهنم نمیرسه
از تغییر متغیرهای مثلثاتی هم استفاده میکنم ولی خیلی راه گشا نیستن.

 

[freddy-elec]

سلام بر دوستان عزیز
چاکرم
دوستان لطف میکنند در مورد این سوال راهنمایی کنند.
تو کلید زده گزینه اول ولی من راه حلی به ذهنم نمیرسه
از تغییر متغیرهای مثلثاتی هم استفاده میکنم ولی خیلی راه گشا نیستن.

با گرفتن تغییر متغیر y'^2 برابر u بنظرم حل شه

 

[hts1369]

با گرفتن تغییر متغیر y'^2 برابر u بنظرم حل شه

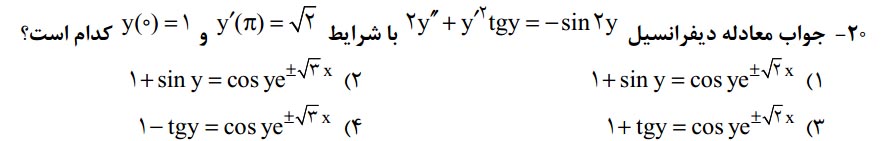
ممنون ولی بعدش چطور عبارتهای تانژانت و سینوس 2y رو باز نویسی کنیم؟

 

[saeeddhk]

ممنون ولی بعدش چطور عبارتهای تانژانت و سینوس 2y رو باز نویسی کنیم؟

sin2y=2siny cosy
sin2y=2tgy/1+tg^y

 

[freddy-elec]

ممنون ولی بعدش چطور عبارتهای تانژانت و سینوس 2y رو باز نویسی کنیم؟

بعد از ساده سازی به یه معادله ی برنولی میرسی که بعد از چند مرحله انتگرال مساله حل میشه،فرمول های لازم هم ایناس:
sin2y=2sinycosy
tgy=siny/cosy

 

[samin_m]

sin2y=2siny cosy
sin2y=2tgy/1+tg^y

بعد از ساده سازی به یه معادله ی برنولی میرسی که بعد از چند مرحله انتگرال مساله حل میشه،فرمول های لازم هم ایناس:
sin2y=2sinycosy
tgy=siny/cosy

وقتی y'^2 برابر با U بشه انوقت "y هم :



میشه توضیح بدید ک معادله بالا ب چ صورت برنولی میشه و چ جوری قابل حا هست؟

ممنون

 

[samin_m]

سلام بر دوستان عزیز
چاکرم
دوستان لطف میکنند در مورد این سوال راهنمایی کنند.
تو کلید زده گزینه اول ولی من راه حلی به ذهنم نمیرسه
از تغییر متغیرهای مثلثاتی هم استفاده میکنم ولی خیلی راه گشا نیستن.

داداش،سوال ه کنکور بوده؟؟؟




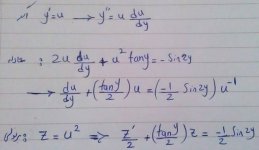
اگه اشتباه نکرده باشم،ب اینجا میرسیم... ک دیگه حوصله نداشتم حلش کنم!!(البته ادامه حلش هم پروسه ای ه واسه خودش)

اگه تا اینجاشو درست حل کردم،مرد میخوام بقیشو حل کنه!!هه هه

 

[hts1369]

sin2y=2siny cosy
sin2y=2tgy/1+tg^y

ممنون شما این پایین رو بخون

بعد از ساده سازی به یه معادله ی برنولی میرسی که بعد از چند مرحله انتگرال مساله حل میشه،فرمول های لازم هم ایناس:
sin2y=2sinycosy
tgy=siny/cosy

ببینید دوستان این رابطه ها که شما نوشتین دارید سینوس و تانژانت رو براساس y بسط میدید
وقتی y (یا مشتقاتش) رو با تغییر متغییر میدیم حالا باید سینوس و تانژانت y رو بر حسب متغییر جدید بسط بدیم
ببینید مشتقات بر حسب y هستن و عبارتهای مثلثاتی هم همچنین(عبارتهای مثلثاتی بر حسب x نیستن که)

داداش،سوال ه کنکور بوده؟؟؟


مشاهده پیوست 172549

اگه اشتباه نکرده باشم،ب اینجا میرسیم... ک دیگه حوصله نداشتم حلش کنم!!(البته ادامه حلش هم پروسه ای ه واسه خودش)

اگه تا اینجاشو درست حل کردم،مرد میخوام بقیشو حل کنه!!هه هه

کنکور ازمایشی سنجش بوده(از مون تعیین سطح)
برا من عجیبه که هیچکدوم از دوستان نمیگن که با جایگزاری شرایط اولیه اصلا به هیچکدوم از گزینه ها نمیرسیم و شاید (احتمال قریب به یقین) سوال و یا گزینه ها اشتباه هستن

 

[samin_m]

ببینید دوستان این رابطه ها که شما نوشتین دارید سینوس و تانژانت رو براساس y بسط میدید
وقتی y (یا مشتقاتش) رو با تغییر متغییر میدیم حالا باید سینوس و تانژانت y رو بر حسب متغییر جدید بسط بدیم
ببینید مشتقات بر حسب y هستن و عبارتهای مثلثاتی هم همچنین(عبارتهای مثلثاتی بر حسب x نیستن که)

حل منو خوندی؟ اگ جاییش مشکلی داره بگو تا برات توضیح بدم داداش

کنکور ازمایشی سنجش بوده(از مون تعیین سطح)
برا من عجیبه که هیچکدوم از دوستان نمیگن که با جایگزاری شرایط اولیه اصلا به هیچکدوم از گزینه ها نمیرسیم و شاید (احتمال قریب به یقین) سوال و یا گزینه ها اشتباه هستن

اما این سوال،اگ راه درستش همینی باشه ک من 30%ش رو نوشتم،باتوجه ب زمان،سرجلسه ارزش حل نداره...

یا مگر اینکه من اشتباه کرده باشم....

 

[hts1369]

حل منو خوندی؟ اگ جاییش مشکلی داره بگو تا برات توضیح بدم داداش




اما این سوال،اگ راه درستش همینی باشه ک من 30%ش رو نوشتم،باتوجه ب زمان،سرجلسه ارزش حل نداره...

یا مگر اینکه من اشتباه کرده باشم....

بله خوندم
شما یکبار دیگه اون چیزی که من گفتم رو بخونید
یه جور دیگه میگم:ببینید اون حل که شما نوشتین ایراد داره.
شما وقتی تغییر متغییر میدین باید تمام عبارتهارو بر حسب متغییر جدید بنویسید
شما لطف کنید و بگید که میخواهید بجای tanyو sin2y چه چیزی بر حسب u مینویسید
بودن یا نبودن y؟؟
مساله این است

 

[samin_m]

بله خوندم
شما یکبار دیگه اون چیزی که من گفتم رو بخونید
یه جور دیگه میگم:ببینید اون حل که شما نوشتین ایراد داره.
شما وقتی تغییر متغییر میدین باید تمام عبارتهارو بر حسب متغییر جدید بنویسید
شما لطف کنید و بگید که میخواهید بجای tanyو sin2y چه چیزی بر حسب u مینویسید
بودن یا نبودن y؟؟
مساله این است

ببین داداش،u تابعی برحسب x هست و y هم همینطور

و خب چون ما توی معادله x به صورت مستقیم نداریم ک مارو درگیر تبدیل x و y بکنه،با توجه به قائده زنجیری (همونطوری ک توی تبدیل y'^2 نوشتم).ما u رو تابعی برحسب y در نظر میگیریم..

در نتیجه معادله مرتبه اول بدست میاریم و حلش میکنیم(جواب برحسب u و y هست)،بعد با جای گذاری مجد0د y'=u دوباره به یه معادله درجه اول میرسیم ک با حلش،x توی جواب ظاهر میشه(جواب y برحسب x)

امیدوارم ک خوب توضیح داده باشم

 

[hts1369]

ببین داداش،u تابعی برحسب x هست و y هم همینطور

و خب چون ما توی معادله x به صورت مستقیم نداریم ک مارو درگیر تبدیل x و y بکنه،با توجه به قائده زنجیری (همونطوری ک توی تبدیل y'^2 نوشتم).ما u رو تابعی برحسب y در نظر میگیریم..

در نتیجه معادله مرتبه اول بدست میاریم و حلش میکنیم(جواب برحسب u و y هست)،بعد با جای گذاری مجد0د y'=u دوباره به یه معادله درجه اول میرسیم ک با حلش،x توی جواب ظاهر میشه(جواب y برحسب x)

امیدوارم ک خوب توضیح داده باشم

بله ممنون
من صبح با این روش حل میکردم ولی در محاسبه یکی از پارامترهای ازاد اشتباه میکردم و به جوابی با این فرم نمیرسیدم واسه این دیگه خیلی اینجوری سوال رو حل نمیکردم
الان یه بار دیگه حلش کردم البته باز هم میگم که شرایط اولیه رو اشتباه دادن ولی شرایطی که برای مشتق (وای پریم) دادن درسته و با استفاده از اون تقریبا میشه به گزینه صحیح رسید.
با تغییر متغیر سوال رو حل میکنیم. و بعد به معادله برنولی میرسیم و بعد به خطی مرتبه اول
با شرایط اولیه دیگه نمیشه متغییر ازاد دوم (d )رو بدست اورد(بدست میاد ولی یه چیز خیلی بدفرم میشه)
ولی اگه y(0) =0
رو بزاریم متغییر ازاد دوم هم صفر میشه و به گزینه اول میرسیم.

 

[aysan 00500]

ممنون شما این پایین رو بخون

ببینید دوستان این رابطه ها که شما نوشتین دارید سینوس و تانژانت رو براساس y بسط میدید
وقتی y (یا مشتقاتش) رو با تغییر متغییر میدیم حالا باید سینوس و تانژانت y رو بر حسب متغییر جدید بسط بدیم
ببینید مشتقات بر حسب y هستن و عبارتهای مثلثاتی هم همچنین(عبارتهای مثلثاتی بر حسب x نیستن که)


کنکور ازمایشی سنجش بوده(از مون تعیین سطح)
برا من عجیبه که هیچکدوم از دوستان نمیگن که با جایگزاری شرایط اولیه اصلا به هیچکدوم از گزینه ها نمیرسیم و شاید (احتمال قریب به یقین) سوال و یا گزینه ها اشتباه هستن

مگه نمیگی سواله کنکور آزمایشی سنجش بوده پاسخ تشریحی نداره ؟ اگه نداشته باشه که خیلی بده جزء ضعف هاش محسوب میشه .

 

[hts1369]

مگه نمیگی سواله کنکور آزمایشی سنجش بوده پاسخ تشریحی نداره ؟ اگه نداشته باشه که خیلی بده جزء ضعف هاش محسوب میشه .

این ازمون تعیین سطح سازمان سنجش هست که رایگان بودش
من فقط کلید نهایی رو دارم اگه احیانا کسی جواب تشریحی سوالهارو داره لطف کنه و بزاره

 

[bio_elec]

سلام
میشه این تابع رو در نقطه pi مقدارش رو حساب کنید؟مقدار حدچپ وراست رو میشه برام دقیق حساب کنید در این نقطه, طبق صورت سوال؟

 

[samin_m]

سلام دوستان

میشه دلیل و اثبات این تغییر رو توضیح بدید؟

ممنونم...

 

[Mr.Perfect]

سلام
میشه این تابع رو در نقطه pi مقدارش رو حساب کنید؟مقدار حدچپ وراست رو میشه برام دقیق حساب کنید در این نقطه, طبق صورت سوال؟​

http://www.www.www.iran-eng.ir/attachment.php?attachmentid=172864&d=1380465389&thumb=1

سلام...
سری فوریه در نقاظ ناپیوستگی به میانگین حد چپ و حد راست میل میکنه...

پس داریم:
((pi^2+pi)+(pi^2-pi)) تقسیم بر 2 = که میشه pi^2

 

[bio_elec]

سلام...
سری فوریه در نقاظ ناپیوستگی به میانگین حد چپ و حد راست میل میکنه...

پس داریم:
((pi^2+pi)+(pi^2-pi)) تقسیم بر 2 = که میشه pi^2

من این مقادیرو میگم:
f(pi+)barabre?
f(pi-)barabre?

 

[.V A H I D.]

من این مقادیرو میگم:
f(pi+)barabre?
f(pi-)barabre?

تو صورت سوال گفته دوره تناوب 2piهستش پس میتونین به جای حد راست درpi از حد راست درpi- استفاده کنین که میشهi^2+pi
برای حد چپpi از خود pi استفاده کنیدi^2-pi
که در نهایت جواب میشهi^2

 

[hts1369]

سلام دوستان

میشه دلیل و اثبات این تغییر رو توضیح بدید؟

ممنونم...

مشاهده پیوست 172868

سلام بفرمایید
وقتی معادله بر حسب x خطی هست و ما میتونیم معادلات خطی رو راحت حل کنیم ولی معادلات غیر خطی معمولا حلشون سختر هست معادله رو به این صورت در میاریم تا بتونیم حلش کنیم.

من این مقادیرو میگم:
f(pi+)barabre?
f(pi-)barabre?

خب این دوستمون همینهارو بدست اورده دیگه
با اجازه من دوباره مینویسم.
برای pi+ =pi^2+pi
برای pi-=pi^2-pi

 

[bio_elec]

خب این دوستمون همینهارو بدست اورده دیگه
با اجازه من دوباره مینویسم.
برای pi+ =pi^2+pi
برای pi-=pi^2-pi[/QUOTE]

من میخواستم بدونه استفاده از نقطه منفی پی و فقط با استفاده از نقطه پی بگین.
با استفاده از نقطه پی:
حد چپ pi^2-pi
حد راست همpi^2-pi
میشه.
منظورم این بود ولی...

 

[hts1369]

خب این دوستمون همینهارو بدست اورده دیگه
با اجازه من دوباره مینویسم.
برای pi+ =pi^2+pi
برای pi-=pi^2-pi

من میخواستم بدونه استفاده از نقطه منفی پی و فقط با استفاده از نقطه پی بگین.
با استفاده از نقطه پی:
حد چپ pi^2-pi
حد راست همpi^2-pi
میشه.
منظورم این بود ولی...[/QUOTE]

ببین دوست عزیز در این سوال باید ما مقادیری کمی بیشتر از پی و کمی کمتر از پی رو در نظر بگیریم.درسته؟
مقدار کمتر از پی (همون طور که از منحنی مشخص هست) با مقدار تابع در نقطه پی برابر هست
اما
برای مقدار تابع در مقداری بیشتر از پی چی میتونیم بگیم.
شما از روی منحنی چی میبینی؟
میبینیم که با مقدار تابع در منفی پی برابر هست.
امیدوارم توضیح قانع کننده باشه

 

[bio_elec]

ببین دوست عزیز در این سوال باید ما مقادیری کمی بیشتر از پی و کمی کمتر از پی رو در نظر بگیریم.درسته؟
مقدار کمتر از پی (همون طور که از منحنی مشخص هست) با مقدار تابع در نقطه پی برابر هست
اما
برای مقدار تابع در مقداری بیشتر از پی چی میتونیم بگیم.
شما از روی منحنی چی میبینی؟
میبینیم که با مقدار تابع در منفی پی برابر هست.
امیدوارم توضیح قانع کننده باشه

بله ممنون

 

[bio_elec]

لطفا این سوالا رو ببینین راهنمایی بفرمایین که چکار کنم.ممنون

 

[hts1369]

لطفا این سوالا رو ببینین راهنمایی بفرمایین که چکار کنم.ممنون
مشاهده پیوست 173138

سلا
بفرمایید
سوال دومتون رو اگه میشه باز نویسی کنید یا توضیح بدین که منظورتون چیه و چه چیزی رو میخواهید شاید بتونیم کمک کنیم

 

[samin_m]

دوستان این سوال بسیار ساده هست(کنکور پارسال)

میخواستم بدونم ب نظر شما اشتباه حل نکرده؟

 

[890031156]

سلام برا دوستانی که برا آمار و احتمال برنامه دارن.
http://s2.picofile.com/file/7956863438/amar_va_ehtemal_bargh.pdf.html

 

[bio_elec]

سلا
بفرمایید
سوال دومتون رو اگه میشه باز نویسی کنید یا توضیح بدین که منظورتون چیه و چه چیزی رو میخواهید شاید بتونیم کمک کنیم

سلام
ممنونم
سوال2:
d(L(y"))/dx?
مربوط به این سوال:
ty"+(1-t)y'+ny=0
که لاپلاس میخواست در این سوال.

 

[hts1369]

دوستان این سوال بسیار ساده هست(کنکور پارسال)

میخواستم بدونم ب نظر شما اشتباه حل نکرده؟

مشاهده پیوست 173149مشاهده پیوست 173150

سلام
درست حل شده
چرا فکر میکنیذ اشتباه هست؟

سلام
ممنونم
سوال2:
d(L(y"))/dx?
مربوط به این سوال:
ty"+(1-t)y'+ny=0
که لاپلاس میخواست در این سوال.

سلام
خاهش میکنم
شما قضایای تبدیل لاپلاس رو خوب خوندین
این جزوه تبدیل لاپلاس مشتق هست.
کتاب معادلاتتون این بحث رو نگاه کنید ایشالا نتیجه میگیرید
یا علی

 

[samin_m]

سلام
درست حل شده
چرا فکر میکنیذ اشتباه هست؟

فکرکردم رابطه پاسوال رو اشتباه نوشته!