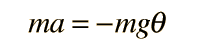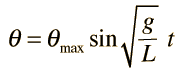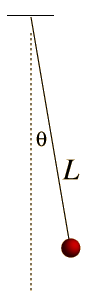mohammadloo
عضو جدید
Simple Pendulum
A simple pendulum is one which can be considered to be a point mass suspended from a string or rod of negligible mass. It is a resonant system with a single resonant frequency. For small amplitudes, the period of such a pendulum can be approximated by:
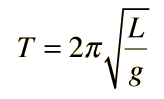 Showfunction cper(){fh=document.forms[0];def();fh.t.value=2*Math.PI*Math.sqrt(fh.L.value*.01/fh.g.value)}function clen(){fh=document.forms[0];def();fh.L.value=100*fh.t.value*fh.t.value*fh.g.value/(4*Math.PI*Math.PI)}function cg(){fh=document.forms[0];def();fh.g.value=fh.L.value*.01*(4*Math.PI*Math.PI)/(fh.t.value*fh.t.value)}function ul(l){fh=document.forms[0];fh.L.value=l;fh.Lm.value=l/100}function def(){fh=document.forms[0];if (fh.L.value==0)fh.L.value=25;if (fh.g.value==0)fh.g.value=9.8;if (fh.t.value==0)fh.t.value=1}For pendulum length
Showfunction cper(){fh=document.forms[0];def();fh.t.value=2*Math.PI*Math.sqrt(fh.L.value*.01/fh.g.value)}function clen(){fh=document.forms[0];def();fh.L.value=100*fh.t.value*fh.t.value*fh.g.value/(4*Math.PI*Math.PI)}function cg(){fh=document.forms[0];def();fh.g.value=fh.L.value*.01*(4*Math.PI*Math.PI)/(fh.t.value*fh.t.value)}function ul(l){fh=document.forms[0];fh.L.value=l;fh.Lm.value=l/100}function def(){fh=document.forms[0];if (fh.L.value==0)fh.L.value=25;if (fh.g.value==0)fh.g.value=9.8;if (fh.t.value==0)fh.t.value=1}For pendulum length
[SIZE=+2]L = [/SIZE]cm = m and acceleration of gravity
[SIZE=+2]g = [/SIZE]m/s2the pendulum period is
[SIZE=+2]T = [/SIZE]s(Enter data for two of the variables and then click on the active text for the third variable to calculate it.)
This expression for period is reasonably accurate for angles of a few degrees, but the treatment of the large amplitude pendulum is much more complex.
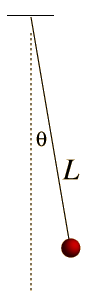 If the rod is not of negligible mass, then it must be treated as a physical pendulum.
If the rod is not of negligible mass, then it must be treated as a physical pendulum.
Pendulum Motion
The motion of a simple pendulum is like simple harmonic motion in that the equation for the angular displacement is
 Showwhich is the same form as the motion of a mass on a spring:
Showwhich is the same form as the motion of a mass on a spring:
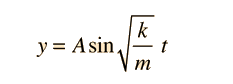 The anglular frequency of the motion is then given by
The anglular frequency of the motion is then given by
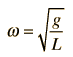 compared to
compared to
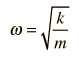 for a mass on a spring.
for a mass on a spring.
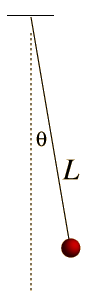 The frequency of the pendulum in Hz is given by
The frequency of the pendulum in Hz is given by
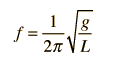 and the period of motion is then
and the period of motion is then
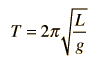 Period of Simple Pendulum
Period of Simple Pendulum
A point mass hanging on a massless string is an idealized example of a simple pendulum. When displaced from its equilibrium point, the restoring force which brings it back to the center is given by:
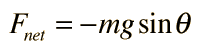 ShowFor small angles θ, we can use the approximation
ShowFor small angles θ, we can use the approximation
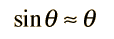 Showin which case Newton's 2nd law takes the form
Showin which case Newton's 2nd law takes the form
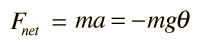 Even in this approximate case, the solution of the equation uses calculus and differential equations. The differential equation is
Even in this approximate case, the solution of the equation uses calculus and differential equations. The differential equation is
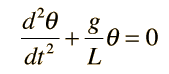 and for small angles θ the solution is:
and for small angles θ the solution is:
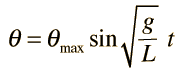
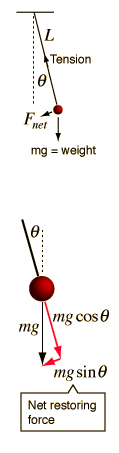 Pendulum Equation
Pendulum Equation
The equation of motion for the simple pendulum for sufficiently small amplitude has the form
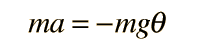 which when put in angular form becomes
which when put in angular form becomes
 This differential equation is like that for the simple harmonic oscillator and has the solution:
This differential equation is like that for the simple harmonic oscillator and has the solution:
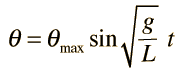
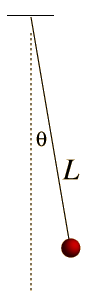
A simple pendulum is one which can be considered to be a point mass suspended from a string or rod of negligible mass. It is a resonant system with a single resonant frequency. For small amplitudes, the period of such a pendulum can be approximated by:
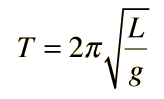
[SIZE=+2]L = [/SIZE]cm = m and acceleration of gravity
[SIZE=+2]g = [/SIZE]m/s2the pendulum period is
[SIZE=+2]T = [/SIZE]s(Enter data for two of the variables and then click on the active text for the third variable to calculate it.)
This expression for period is reasonably accurate for angles of a few degrees, but the treatment of the large amplitude pendulum is much more complex.
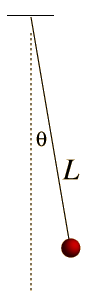
Pendulum Motion
The motion of a simple pendulum is like simple harmonic motion in that the equation for the angular displacement is

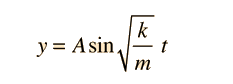
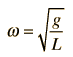
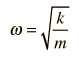
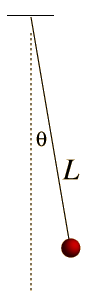
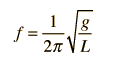
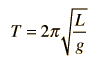
A point mass hanging on a massless string is an idealized example of a simple pendulum. When displaced from its equilibrium point, the restoring force which brings it back to the center is given by:
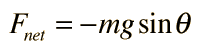
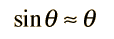
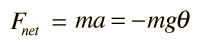
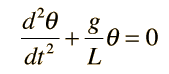
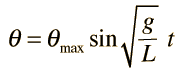
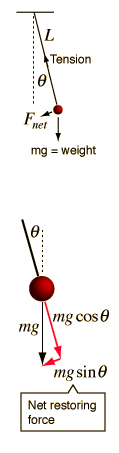
The equation of motion for the simple pendulum for sufficiently small amplitude has the form