برج هانوی , معمایی است که از سه میله و N دیسک با اندازه های متفاوت . فرض شود که اگر دیسکی روی یک میله باشد , فقط دیسکی که قطر آن کوچکتر است می تواند بالای آن قرار گیرد مسئله چنین است که هر بار فقط یک دیسک انتقال یابد .
را حل : این مسئله با استفاده از یک الگوریتم باز گشتی حل می شود .
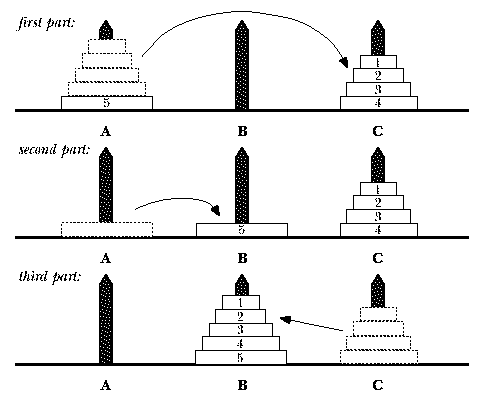
-اگر فقط یک دیسک باشد آنگاه آن را به میله مورد نظر انتقال می دهیم .
-اگر n > 1 باشد ; برای این کار n-1 دیسک بالای میله 1 را به میله 2 انتقال می دهیم . حالا دیسک پایینی میله 1 را ثابت باقی می ماند . حال دیسک باقیمانده در در میله 1 را به میله 3 منتقل میکنیم . سرانجام بار دیگر بصورت بازگشتی الگوریتم را فرا خانده تا n - 1 دیسک میله دو را به 3 منتقل کند .
اکنون موفق شدیم n دیسک را از میله 1 به 3 منقل کنیم .
این مسئله در درسهایی مانند ساختمان گسسته و ساختمان داده مورد بحث وبررسی قرار می گیرد .را حل : این مسئله با استفاده از یک الگوریتم باز گشتی حل می شود .
-اگر فقط یک دیسک باشد آنگاه آن را به میله مورد نظر انتقال می دهیم .
-اگر n > 1 باشد ; برای این کار n-1 دیسک بالای میله 1 را به میله 2 انتقال می دهیم . حالا دیسک پایینی میله 1 را ثابت باقی می ماند . حال دیسک باقیمانده در در میله 1 را به میله 3 منتقل میکنیم . سرانجام بار دیگر بصورت بازگشتی الگوریتم را فرا خانده تا n - 1 دیسک میله دو را به 3 منتقل کند .
اکنون موفق شدیم n دیسک را از میله 1 به 3 منقل کنیم .
PHP:
[IMG]http://www.cs.berkeley.edu/%7Ebh/v1ch8/hanoi4.gif[/IMG]/*
Algorithmic solution is as follows
1) if TopN==1, move the single disc from A to C and stop.
2) Move the top n-1 discs from A to B, using C as Inter.
3) Move the remaining disc from A to C.
4) Move the n-1 discs from B to C, using A as destination(dest).
*/
#include <stdio.h>
#include <conio.h>void tower(int,char,char,char); /*prototype*/
int main()
{
int ndisk;
clrscr();
printf("\n Enter number of disks <<<::: ");
scanf("%d",&ndisk);
tower(ndisk,'A','B','C'); /*Calling Function*/
getch();
return 0;
} /* End of program */
/********************************************/
// src = Source | aux = Auxiliry | dest = Destination
void tower(int topN, char src,char aux,char dest)
{
if(topN == 1)
{
printf("\n Disk 1 from %c to %c ",src,dest);
}
else
{
tower(topN-1,src,dest,aux); //src to aux
printf("\n Disk %d from %c to %c ",topN,src,dest);
tower(topN-1,aux,src,dest); //aux to dest
}
}http://www.www.www.iran-eng.ir/image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAV4AAAFeCAIAAABCSeBNAAAgAElEQVR4nO2dz4vcRvrGBcnBm+CYJNgYe00aJ16PEnBsRMAd/yBm4uBhaewd2azDsMYQEBsfcrIvuswcdnxpnQPKwRhfhA8NwehgCIEhTG46+rIYDM3gYw77F8z38Nr1LZdK1eqeqtZbnedDYUbdUul537f0VEk90w4CAAAAAAAAAAAAAAAAAAAAAAAAAAAAfKIoiuhNqqqy1XlUoygKW53XKcsyy7KmtyYenqapojZNU9saX6GkPc9zRycCYEayLEuSpJSw2Dl1SOPeeufWqapKiKQfLLqkgpJ2esXRuQCYhSzL6oOSxmscx0mS0GYcx/KcXxRFWZZJktAqoyzLKIpo5zr0rrwp9yavI4QS2UfoLMpbQpugqqokSYqiqM/AdArRQ5ZlBrV1FAFKEhTltByI41i8VRQFnVF2RiXtSooA6B6tNdAr8pwmLgN6i5bBYgFPV0KSJNrrTR739d7SNKWLmS45mqjlSyvLMmFDijb5LDQJa2OUrUFct+1naRJAdqa8Fcex0BwEgbI+kt1N0aakPUkSrBoAL5QRSZt0xdIrNBUrR2mfGjRNffLr9d7Eu3Txy3N+URR1r5G1aTF4RH1P87MPrQAx/4ugsizTLlUMCxMYAeBO06pBvKishA0vtrEG7YHynjSl02ysvdPRCqYrnNYyQRC0vLXRdiWj7EDi8zxP05RuE4LXSwbtUwnDPYLSc57nuKEAvJhoDfLaXjCzNWh7S5JEvjbEZE4XYRvBweubFPPDTuUCpvM27awVIHqgtUmaprN9ijHRlQDomInWIC+5xdOEma1B25v5Eb1y314XXJ+xxfMLLeKJQNMOWgHaDukt+eZLLFjiODZc/EoU9JyypR4A5sFEawiki1aM+5mtQdub2C0IgjRN6W5CflH+uS64PvnXzUL0WVWV8kzUjNhH/o0PgzeJoMyfgCg9xHHs7oNSAAAAAAAAAAAAAAAAAACABaEsq6LY7loFcEVZVv3+kFqaPu5aDvCEsqyCYGM4fNK1EOCK4fBJkuRlWZVlVVXPu5YDfCBNHwfBRhz/CGtYYPr9YVniN23ANNCIGQ6fwBoWmo1+fxgEG0GwgVUDmIKZrWFzc3Nzc9O6HsiwzStHoJvHaQ9mEhdkdMDM1iD+PLZbIKM9M9xcMIkLMjoA1rBIMhTo6aP0wtT3FEzigowOmM0ayrKkxVW3XxMKGWbkm4g8/2XaGwomcUFGN8jWQJ+BtzmKEkTJcqkOMvZKUWzTM8h+fygeOqDK/srgThRFOzs7Ozs73a6vIMMpTOKCDJ+Iomh3d3d3d7fzakGGO5jEBRneQGsqSlOHt16Q4RQmcUGGT1BqKE0d3npBhlOYxAUZfKHv3pYJw5C+lj/P8yzLwjBUdpiPp9K9H1WrwztAJjKswyQuyODLYLB+5syjzz9/KtrBgw8Mm2fOPBoM1uejbVdiPmfkLMM6TOKCDKYMButLSy+OHNkVLQheGjaXll7AGhYDJnFBBlNgDb7IsA6TuCCDKbAGX2RYh0lckMEUWIMvMqzDJC7IYAqswRcZ1mESF2QwBdbgiwzrMIkLMpgCa/BFhnWYxAUZTIE1+CLDOkziggymwBp8kWEdJnFBBlNgDb7IsA6TuCCDKbAGX2RYh0lckMGL6jXLy/fC8NePP/6vaAcO/G7YDMNfl5fvicOdimRSLSYyrMMkrvnLGI/H1Zvs27fPsFlV1Xg8no+2jqmq6tyli/3Vlf7qylJ048TJNbkdOz4wbJ44ubYU3aBjz1266NQd/rRjdz4wiWv+MuI4XV6+99VX/xHt8OF/GTaXl+/FcTofbR1TVVV/deW9u/oWXP/CsCm3/uoKrMFfmMQ1fxmcb6I7BtbgowzrMIkL1sAIWIOPMqzDJC5YAyNgDT7KsA6TuGANjIA1+CjDOkzigjUwAtbgowzrMIkL1sAIWIOPMqzDJC5YAyNgDT7KsA6TuGANjIA1+CjDOkzigjUwAtbgowzrMIkL1sAIWIOPMqzDJC5YAyNgDT7KsA6TuGAN3VOW5fra8vra8p1r58MwXPryM23rRZ8YNuUWhuGda+epTxf/292fduzOB6dxicFmblfCDw2bTW2GwTYej6/eunllLb6yFn/66eqJk2uf/O3fov31o9uGzRMn1z79dJWOvXrr5gL+FWae54+uH33x3bvPbu8vb7zf1B5e3mfYVNqz2/tffPfuo+tH8zy3LpjJNclEhnWcxiUGm7lt/+Ntw6a2zTbYqqrqDy4f+X7lyPcrx/55SWnvffW5YZMaHdsfXHb9XQQdkOf507VDu3feMreX3waGTW17unYI1uAdrq2B1WDz5Sa6G7hVayJMrkkmMqwDa4A1vIJbtSbC5JpkIsM6sAZYwyu4VWsiTK5JJjKsA2uANbyCW7UmwuSaZCLDOrAGWMMruFVrIkyuSSYyrANrgDW8glu1JsLkmmQiwzqwBljDK7hVayJMrkkmMqwDa4A1vIJbtSbC5JpkIsM6sAZYwyu4VWsiTK5JJjKsA2uANbyCW7UmwuSaZCLDOrAGWMMr8jy/Pzj+8/UPzO3BN+8YNrXt/uD4tNUaTULZp+Uh08JEhnU6j4vbYMuy7PSFs8fii9p24OIpw6bcTl84m2UZkypbY2trq9fr9Xq90CrU59bWVnsldFRkFYprqoQwkWEdDnFxG2zWZYRdV9kmo9Go1+t97YBer9feRyHDKUziggyfGI1GURS5SFMURVNVCzLcwSQuyPAJJmmCDKcwiQsyfILJ4goynMIkLsjwjJDBAyrIcA2TuCDDMyZ+RjUDkLFHGdZhEhdkAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAHFEWh/O63xe+uqv9ieVEUtjqvU5ZllmVNb008PE1TRW2aprY1vkJJu4uvxhNUVeWuCvNMWvBmHZMkqe/QZvTWE2J32NcxjEy+ZFmWJEkpYbFz6pDGvfXOrVNVlRBJP7gbLkra6RVH55Ijsl6FeSZNnIU2kySJokjZJ4qiNgGS1CRJRBWsq/WeLMvqg5KSFccxGTP9LM82RVFQZsluy7KMokjr4nS4XEKlN3kGE0rkatFZlLeENkFVVUmSFEVRn4HpFKKHLMsMausoApQkKMppORDHsXirKAo6ozz+lLQrKbJLU+eKMCUtlGd6sSiKqqriOI7juOWVP1XS6hWh0RXHsdKtcnZlB+pZDkEZtwpKFZTayUNO1t/UOYVWXwMaRiZrtNZAr8iTjKgovUVrMLFMomySB9dPIQ/Nem9pmlLKKMVUe/nSyrJM2JCiTT4L2b82RtkaRO3bz9IkgMaB8hYNTTFelfWR7G6KNiXtSZI4XTU0+Y4QVk8L/SAqRe+2H9ztk0aOI3dOZ8zzXL6k21iSbA3acVsXqcQrXICOopPWRzW9Xr8ogilHJmuUlNEmXbH0ChmecpTWiZuGoPx6vTfxLl388uAriqJeFVmblvaV0IYmoxUgplkRVJZl2qWKYWEyzztPJRsTlyeUFrrlEYe0H9x7SRqdWnuulgsrcaKJxQ0a5kURgvyuWB2TrzVdFOYseeYRTasGOSn1eLQvtrEGc/oo9aIA2jsdrWCqE61lgoYHVHWFTSOjaQcSn+d5mqZ08QSvJxDtnGYYykrPeZ7P/4aiaYdMgl6ZyhqmSlq9W1pu1AW3vJGRPWii5qYBQALEGenZKoVAdqbNp/aMLUcmRyZag7y2F8xsDdrekiSRrw1hyVSMNoKD16s78yMlZXjReZt21goQPdAMkKbpbA/kJ7qSRSZagzYtM1vDVEmjt8T/gjMej3d3d9s/eanPw0KqdqQpGMaSeIpBqRDTFdH+ogjajUyOTLQGeeEknibMbA3a3gx3g+Jd+dGDsmd9PhHurkU8EWjaQStA2yG9Jd98iWkhjmPDxa9EkWVZh6sGQknLzNYgThq0SxrtRr4QvL5X1wpWsqS9XxBStSOt3qGIUdmHDieRTWsBRVU9S9OOTF5MtIZAumjNN59trEHbm9gtCII0TWV7ls8iHEQRXJ/86yURfdJn2vXOmxD7yCtMgzeJoMxLR6WH9k/+Z6CNNdTTshdrmCpp8qmz188CmwTTtSrerSdNfqTdNNIEylgSu4kXlajlYSYnh2TUs9RmZAIArOHf4hwAAAAAAAAAAAAAAADAm5RlFcc/9vvD4fBJ11qAQ5Ik7/eHafq4ayHAGzaKYpsMIo5/7FoMcMTGcPgEVQZtKYrtN6eRja6UAHfk+S9JktOvIf/xx/+wPATTUVXPYQ0LSRz/WJZVmj7GDQWYjY2ynPpXODc3Nzc3N12ogQxb9PtDcduYJPkMEwCTuCCjEzaKYnuGw8SfmnYLZBjo94dvmv5GVT2fqgcmcUHGXKH7iNl8IWCTJsgwkKaPFWuYdnnIJC7ImB/kC9POIYKyLGlx1e0fukCGmbKsxE1EUWxPe0PBJC7ImCtx/GMQbLzZgrKs+v1hm8MpQZQsdyIhY++8doSNfn9IMwGq7LUM7kRRtLOzs7Oz0+36CjKcwiQuyPCJKIro0/LOqwUZ7mASF2R4A62pKE0d3npBhlOYxAUZPkGpoTR1eOsFGU5hEhdk+ATddFGaOrz1ggynMIkLMjxjVwIymMiwDpO4IMMnmKQJMpzCJC7I8AkmaYIMpzCJCzJ8gkmaIMMpTOKCDJ9gkibIcAqTuCDDJ5ikCTKcwiQuyPAJJmmCDKcwiQsyfIJJmiDDKUziggyfYJImyHAKk7ggwyeYpAkynMIkLsjwCSZpggynMIkLMnyCSZogwylM4oIMXlTN7Nu3z7Cp4FQkk2oxkWEdJnFBBiOqqjp36WJ/dUXbDp762LApt3OXLjp1BybVYiLDOkziggxGVFXVX115766+Bde/MGzKrb+6AmvwFyZxQQYjYA0+yrAOk7gggxGwBh9lWIdJXJDBCFiDjzKswyQuyGAErMFHGdZhEhdkMALW4KMM6zCJCzIYAWvwUYZ1mMQFGYyANfgowzpM4oIMRsAafJRhHSZxQQYjYA0+yrAOk7gggxGwBh9lWIdJXJDBCFiDjzKswyQuyOiesizX15bX15bvXDsfhuHSl59pWy/6xLAptzAM71w7T33u8X8QvXv34WCwLrfDh68YNgeD9bt3H1pKzAQWYNDMP71isJnblfBDw2ZTm2Gwjcfjq7duXlmLte3gyY8Mm3K7euvmeDzeS2Y4kuf5o+tHX3z37rPb+8sb7ze1h5f3GTaV9uz2/hffvfvo+tE8z/eibTBYP3Xqt6WlF6IdOPC7YfPUqd8Gg3VbmTGzANYw//SKwWZu2/9427CpbbMNtqqq+oPLR75f0ba//D0ybMqtP7js+rsIOiDP86drh3bvvGVuL78NDJva9nTt0N6tYWnpxZEju6IFwUvD5tLSC1hDe+afXm6DzZeb6G7gVi0ZWINTYA2wBhPcqiUDa3AKrAHWYIJbtWRgDU6BNcAaTHCrlgyswSmwBliDCW7VkoE1OAXWAGswwa1aMrAGp8AaYA0muFVLBtbgFFgDrMEEt2rJwBqcAmuANZjgVi0ZWINTYA2wBhPcqiUDa3AKrAHWYCLP8/uD4z9f/8DcHnzzjmFT2+4Pjk9brdGbnD//Qxj+dPLkz6IdPPjAsBmGP50//4PSyQw5GU1C2aflIZ3TeXq5DbYsy05fOHssvqhtBy6eMmzK7fSFs1mWMamyNba2tnq9Xq/XC61CfW5tbbVXQkdFErOdWu6B4poqIXUZe2cGGdbhkF5ug826jLDrKttkNBr1er2vHdDr9dr7KGQ4hUlckOETo9EoiiIXaYqiaKpqQYY7mMQFGT7BJE2Q4RQmcUGGTzBZXEGGU5jEBRmeEfJ48AYZTmESF2R4xsTP3mYAMvYowzpM4oIMAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAOCANE2V3/221XNRFPVfLLfVuZYsy5r+6/Q2/6V6XW1RFLY16iUlSeLuRPVCWPx6sjknLcsy7c+CNoWuj/k0TW2qlFCSv8fvQJwrJLeUsNi56FCcwmLnU8lo40qkkIrnWi11Lk6RJIk738yyLEkSpyWeT9LSNI3jWH5F6w4TqapKSKUf3H2Vo5L8YFbNHRBFUb2cRVHQ5UQlJ+eL41jsSfNzHMdUqizLoihqilk5Be0s5klxVFmWYsIRP9BZ5LmoKArqQZGd53lRFEmS1MtM5xI90HXYpFbxEUWAPPrlHkTnSnS0fxzH9XWBolMZ9BbJsqwerCJMm+eyLClXdC3JcdV7MyRNXkfI5VacUXlLmzQFJWl0ItGPUouJKDKUVCj66xeFdmQqyW85S7FAaw2knipEgYnrVi4n1S+QVvLaxaR8CpFNOV90kTRdPKIw4hA6tTYcGs3Ki4o1CF/TFkkunghKCBAhE2SdeZ7TipS8UsyiQrMync7564a11iALq4cZvL5TEJWiuJIk0V5p5qSlaSrmmOB1+MpME0hLJ23S8jyfeJHL1qAdaRMT1TQwqOiicMoqSbkolD5lAUmS+LRqkDcpMK1fBEFA03J9f0I7BA29JUlCRiuOEhMUVYJ2oG9wH4/Hhii0jiC/S2HW9Rt2NgsQk4aQTa+Lr5wX0dXvY+c8dShFoU1ZGElVjtI+NWhSXk+a9l26+OX7bW1FtElrGl1t0AYoo5Uhxq0ILcuy+sMC86DyxgjqNK0atBdzfWTIr0y0BuVw2l9cVPQ0iGZgKkD764dqQxNdUFu8iPMqCrVhyiJpB+U/mBDzp3JsvavsNcrrTFYNsiO3HANtrKFp8Ig9KYFivVnfQStYLM3aoB1phv21A4POSP4evK6atnaGgar0nOe59zcUTasG5e5uKmtQ0pokifDgPM/ry3V5zTkRsTY2zHX14VWvtBwRCVBWDUVRyJ2kaUrGRF0JHxmPx7u7u+3nOsNd0h6ZaA3aPM9sDdreqNb1lYX2gt+7nxpGmhbDwKC6pGk626cYe1nsdMxEa1BuL5sm5KD1DYW4TxOvUNLrMpTHV012qx1e8uDQTu9NY0WOiASMx+M//vifkgfap648z3PhI00TYD0c1x/4ma1BPrsIc2Zr0PamPC2qHx5IaTQMJLnQEz/WqY80M4aBQW/Jt2BiMMRxbLj4lVgMw5gdbVYN9U8TBNNaQ1VVyvOqoFY8uTbKY4imKJS3DI+s5Aei2g7ra1H6QfEFrZ3J0Ylb+qZxQz2I/Z1+fma2hkAX5szWoO1N7BbUPoOUzyIcpClpdBb5XwXRs3akGdAODEWGXCMRmvnpldJDHMcL+H/eARcoz+FBG0qXv4kAAAAAAAAAAAAAAAAAYA6UZRXHP/b7wzz/pWstwAlFsd3vD+VWVc+7FgU8YKMotsuyCoKN4fBJ12KAE8qyEq3fH3YtB7CnLCuxWMCg+TOAEoPpoFVDWeJ3SBaZ4fAJFoZgCqrqOd2CFsX2tMdubm5ubm66UAUZDtiY7TAmcUFGh2xMe4D4I+hugYyJ5Pkvafp4tmOZxAUZ80N+1hAEQb8/nPaegkmaIKMFGzN/MMEkLsiYH/SIgUZMUWxPu2ooy5IWV93+dRBktGNjtsOYxAUZ8+a1I2yIj7vbf1RBCaJkuVUJGXujXlNU2WsZ3ImiaGdnZ2dnp9v1FWQ4hUlckOETURTRN511Xi3IcAeTuCDDG2hNRWnq8NYLMpzCJC7I8AlKDaWpw1svyHAKk7ggwyfopovS1OGtF2Q4hUlckOEZuxKQwUSGdZjEBRk+wSRNkOEUJnFBhk8wSRNkOIVJXJDhE0zSBBlOYRIXZPgEkzRBhlOYxAUZPsEkTZDhFCZxQYZPMEkTZDiFSVyQ4RNM0gQZTmESF2T4BJM0QYZTmMQFGT7BJE2Q4RQmcUGGTzBJE2Q4hUlckOETTNIEGU5hEhdk+ASTNEGGU+YWV9XMvn37DJsKTkUuapUtwyRNkOGU+cRVVdW5Sxf7qyvadvDUx4ZNuZ27dNGpOyxqlS3DJE2Q4ZS5WUN/deW9u/oWXP/CsCm3/uoKrKF7mKQJMpwCa5BZ1CpbhkmaIMMpsAaZRa2yZZikCTKcAmuQWdQqW4ZJmiDDKbAGmUWtsmWYpAkynAJrkFnUKluGSZogwymwBplFrbJlmKQJMpwCa5BZ1CpbhkmaIMMpsAaZRa2yZZikCTKcAmuQWdQqW4ZJmiDDKbAGmUWtsmWYpAkynAJrkFnUKreiLMv1teWJ7Ur4oWGzqe3xfxC9e/fhYLAut8OHrxg2B4P1u3cfWknLeDy+euvmlbVY2w6e/MiwKbert26Ox2Mrkqwz//SKwXbn2vkwDJe+/EzbetEnhk25hWF459p5K4NNy5/aGvI8f3T96Ivv3jW37X+8bdjUtkfXj+Z5vhdtg8H6qVO/LS29EO3Agd8Nm6dO/TYYrFtJS1VV/cHlI9+vaNtf/h4ZNuXWH1x2/YfDMzP/9IrB9uz2/vLG+03t4eV9hk2lPbu938pg0/Jnt4ana4d277xlbi+/DQyb2vZ07dDerWFp6cWRI7uiBcFLw+bS0gub1uDDincvzD+9nAebFlgD02rBGpwCa5gIrIFptWANToE1TATWwLRasAanwBomAmtgWi1Yg1NgDROBNTCtFqzBKbCGicAamFYL1uAUWMNEYA1MqwVrcAqsYSKwBqbVgjU4BdYwEVgD02rBGpwCa5gIrIFptWANToE1TOTPbg33B8d/vv6BuT345h3DprbdHxyftlqjNzl//ocw/OnkyZ9FO3jwgWEzDH86f/4HpZMZcjIajbIsO33h7LH4orYduHjKsCm30xfOZlk2mwzrdJ5ezoOtjrJPy0MWh62trV6v1+v1QqtQn1tbW+2V0FGRxGynlnuguKZKCMmwmArR4XSFsU3IIL2cB9ve4VBlm4xGo16v97UDer1eex+FDKcwiQsyfGI0GkVR5CJNURRNVS3IcAeTuCDDJ5ikCTKcwiQuyPAJJosryHAKk7ggwzOYPJKBDKcwiQsyPGPipzIzABl7lGEdJnFBBgAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAACwTVEUyi9+W/x6svpvlRdFYatzw7mSJKlH0Sauqqrqmp1+X1uSJOJnF//pu2BhCh0EQVmWWZY1vTXx8DRNFbVpmtrW+Aol7S6+k84VWZYlSVJKWOycOqR0WO+86XRN4yaKojYCqIckSURaHCj9f4RUOpG70y1SofdIVVVCJP3gzv2VtAdSxbmTZVldK4URxzHNafSzPBUURUHXD00+ZVnSXK09Bb0rb8q9ydOLfJ2I4UVnUd4S2ppQjIB+FofUIzKnhbw/jmPqx6y5KV3KpFEURRzHSqLcjZuFKXRVVUmSFEVRn4HpFKKHLMsMausoApQkKMqVIUGv0BnlgaekXUkRa7Qjhl6RrU5kh96i1ZEYypQgmmnrp5DTUe8tTVOqMVWC/FvOeJZlYnQq2pqCqr8lW4M2IkNaxBlJYVmWBs30cz1ddc1xHDtddRsikl8MfCs0TcLaGGVrENdte7clAWRnyltk4mJxoayPZHdTtClpT5LEp1VDfZMKSa+QQytHaefbJkeUX6/3Jt6lMaHMq0mSKN/tLWszUN9H2Lk2IgXthSQkGTRT5yR4PB4rp9bqmQ/8C10XbC60wSPqe5orrhUgCiSCyrJMu1QxLEy8MYI6TZOJeLH9sG4zYszXA3k2/Rvo0kqTQMt0KyeSKz1xSDWdpR6jolmbAe0Z5QlzDixGoekKp7VM8OZDXIPCiWNG2YHE53mepindJgSvlwzapxKGewSl5zzPvb+hEC9qR/DMI0bbW5IkcsqEx1Nt2ghuE5fQ3OaaNKwaaDQ3aW6frjzP298G752FKTTdpJjvKJULmM7btLNWgOiB1iZpms72KUb7mYwdE0eMvBITN5kzjxhtb4Z7fvGufEe6x1WDVoOCfBZlH/HEQatZedhGgRum0Pqt6cS4ZmMBCl2fscXzCy3iiUDTDloB2g7pLfnmSwyJOI4NVVOiEEPCAyaOmECqpUjHzCNG25vYLQiCNE3l5/byWcTAarlqUF6Rn4E1aZAPl3sQuyndajXLS3QazU3WIMY65cfdp+vBQhS6PvnXzUL0Sb+iUu+8CbFPJP3Gh8GbRFDmpZ/SQxzHbP9bQ8AO+lCwaxUAAAAAAAAAAAAAAAAAQDek6eOqet61CuCEqnqeJHm/P0zTx11rAV6R578EwUZZ4hPXRWUjz38py4oMomsxwBOq6nkQbMAaFpWyrN60g42ulADv2KDRA2tYXF6tGtL0MVYNoBVJktP952zWsLm5ubm56UAXZNgkSfIg2Oj3h0GwURTb0x7OJC7ImB9FsS2Wl7NZg/jz2G6BDANFsb3HGwomcUHG/KBpRG7TugOTNEGGgeHwyXD4RGzOMAcwiQsyumGGEVOWJS2uuv3rIMgwU5aVWCnIP7c+nEVckNEZwhpqD7QboQRRshyrg4w98frOcSMINui3V1Blr2VwJ4qinZ2dnZ2dbtdXkOEUJnFBhk9EUUTfj9p5tSDDHUziggxvoDUVpanDWy/IcAqTuCDDJyg1lKYOb70gwylM4oIMn6CbLkpTh7dekOGUTuKiL3qXCcMwyzL6OcuyMAyVHeYzgS9qle2zKwEZTGRYZ/5xDQbrZ848+vzzp6IdPPjAsHnmzKPBYH0+2ha1ypZhkibIcEon1rC09OLIkV3RguClYXNp6QWsgRdM0gQZToE1yCxqlS3DJE2Q4RRYg8yiVtkyTNIEGU6BNcgsapUtwyRNkOEUWIPMolbZMkzSBBlOgTXILGqVLcMkTZDhFFiDzKJW2TJM0gQZToE1yCxqlS3DJE2Q4RRYg8yiVtkyTNIEGU6BNcgsapUtwyRNkOEUWIPMolbZMkzSNH8Z4/G4epN9+/YZNquqGo/H89FmnbmlV+RqefleGP768cf/Fe3Agd8Nm2H46/LyPXG4U5FMxjx3mKRp/jLiOF1evvfVV/8R7fDhfxk2l5fvxXE6H23WmU96q6o6d+lif3Wlv+8uvykAAALaSURBVLqyFN04cXJNbseODwybJ06uLUU36Nhzly46dQcmY547TNKEFa9T5mYN/dWV9+7qW3D9C8Om3PqrK7CG7mGSJliDU2ANMkzGPHeYpAnW4BRYgwyTMc8dJmmCNTgF1iDDZMxzh0maYA1OgTXIMBnz3GGSJliDU2ANMkzGPHeYpAnW4BRYgwyTMc8dJmmCNTgF1iDDZMxzh0maYA1OgTXIMBnz3GGSJliDU2ANMkzGPHeYpAnW4BRYgwyTMc8dJmmCNTgF1iDDZMx3Q1mW62vLE9uV8EPDZlNz8R+Qzada4/H46q2bV9biK2vxp5+unji59snf/i3aXz+6bdg8cXLt009X6dirt2769VeYTtMrBtuda+fDMFz68jNt60WfGDblFobhnWvnfR9sTMnz/NH1oy++e9fctv/xtmFT2x5dP5rnuXXB85vWBpePfL9y5PuVY/+8pLT3vvrcsEmNju0PLrv+w2G7OE2vGGzPbu8vb7zf1B5e3mfYVNqz2/t9H2xMyfP86dqh3TtvmdvLbwPDprY9XTvkb7V8WfFax7U1YLB5A6qlBdYAawhgDahWHVgDrCGANaBadWANsIYA1oBq1YE1wBoCWAOqVQfWAGsIYA2oVh1YA6whgDWgWnVgDbCGANaAatWBNcAaAlgDqlUH1gBrCGANqFYdWAOsIYA13B8c//n6B+b24Jt3DJvadn9wfNpqjSah7NPykGkZjUZZlp2+cPZYfFHbDlw8ZdiU2+kLZ7Msm02GdTpPLwabT2xtbfV6vV6vF1qF+tza2mqvhI6KrEJxTZUQkmE9G9PKsA6H9GKw+cRoNOr1el87oNfrtfdRyHAKk7ggwydGo1EURS7SFEXRVNWCDHcwiQsyfIJJmiDDKUziggyfYLK4ggynMIkLMjyDySMZyHAKk7ggwzMmfiozA5CxRxnWYRIXZAAAAAAAAAAAAAAAAAAAAAAAAAAA/In5P4hlxvVHTmMrAAAAAElFTkSuQmCC

