امید بلواری زاده
عضو جدید
سلام دوستان من
من مدتی هست که در آزمایشگاه مرکزی پالایشگاه آبادان مشغول به کار شدم و کارم تعییین چگالی نسبی مواد نفتی هست. متاسفانه با توجه به قدیمی بودن وسایل ما برای تعیین sp.gr محصولات نفتی مثل kerosin , gasoil, ord, mco, و... ابتدا دمای این مایعات رو با ترمومتر اندازه میگیریم سپس با هیدرومتر مناسب sp.gr رو هم یادداشت میکنیم.
سپس با استفاده از جدول23 از astm d1298 یا astm d1250 گراویتی مورد نظر در 60 درجه فارنهایت رو پیدا کرده و یادداشت میکنیم.
مدتی ایست که در پی فرمولی برای محاسبه و کانورت گراویتی هستم که بتوان با دادن دامی محصول و گراویتیش در همان دما (مثلا 70درجه فارنهایت) بتوان گراویتی در 60 درجه فارنهایت رو بدست بیارم.
مطالب زیادی خوندم و فرمولهای زیادی رو از سایتهای خارجی امتحان کردم ولی جواب درستی حاصل نشده چون منحنی تغییرات غیرخطی ایست.
امیدوارم مهندسین ایرانی عزیز بتونید به من کمک کنید.
یرای درستی و صحت کارتون من از روی قسمتی از جدول رو میگذارم تا محاسباتتون دقیق بشه
طبق جدول بالا در دمای 51 درجه گراویتی محصول که با هیدرومتر مشاهده شده 0.751 بوده که طبق جدول گراویتی آن در 60 فارانهایت 0.7466 میباشد.
دوستاان لطف کنید جوابتون رو به ایمیلم ob_z2006@yahoo.com یا با شماره 09374411865 بلواری زاده پیامک کنید.منتظر کمکتون هستمhttp://www.www.www.iran-eng.ir/image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfQAAAFlCAIAAACSjo07AAAbl0lEQVR4nO3dL3DbytfGccHAwsDCC3+wY2R4YWBgkaewsCwvK4xZYWBgmQsNCwsDAi4MDCzcF0i2Je3Zf5JWKx99P9O5M9dxVjrH0mN5pViVAQCoU5VeAQDA9Ah3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCoZLhXAIBMyoZ7waXnprs6AAtHuOeiuzoAC0e456K7OgALR7jnors6AAtHuOeiuzoAC0e45zJldYddVVW7w2TjlfO632gpBVi2JYd7HQROm/3rTCs6SGK4n4oVc49wB5CIcM8lLdwPu1NZUvAR7gASLTncO64uFZKqq9N776qRcAeQiHDPJaW6U3i7iiTcASRSEu6XWQ17vuawqx9qz/I04wgP9X+rM3RKKCVU18puOcbPj3pXpl2NPWcV06Lzc5xvNPUzWo/6hu2vlOfty7v+g18LcWLv0uh+yYAmCsLdswcbY5rdeGM9Z7fb9R6xA8X+rfgMiK/unF2n/7FC8tBfVXtlrC60x0hu0e4gd7y7dqFhY9Y7Zv2HvRb+hYslA4pcfbg3oWDF3CUbrGOz1l7ffaidh6cnXR5rlhR7Hje6uk62N4sRjqz9K9P7rdf9xnpuRIu6i7Vb3sn24LBWw84B7ngZHes/7LXofcaIKxnQ49rDXYrC3vGlfSzc39Gl4aX5kaQJ48jqXveb3pBCSeGVsZPWN164Ra1Be4HYyXbfsEKXU96jk8qPqbo7iqNkQI1rD3fXZ+9+cgmzC3aihsI9KRHiqnNe7unJJXllWiMJ7wzJLWqNeXqa8IbgG1ZsVtTsmviWkfha9N9axDcqpmKgGOHuGH6ecPdcym/NEUWtzGXA+BT2JV1rIb0nTR3uzvUf+loIKxgaE1Dk2sNdnBzomi7crUtFfGKqc619f0Gp8xKd3x/Wos6PzpeV9CfYfcMmTct41n/Ya1GvnvuMKeEO7a493MXJ2tf9xv8BPDbcK+uDfHwgRFTnTjop3aTj5vaUe/+krHc+Ptii7qps9ntHyzzDJpxQ9a5/1GshTbsEj+sJdyh29eHumh+YKtzdH+xHV+c7+Oz+zHEtoDjhLh2pDmhRf1WkVQ0NKzyhrsJ7ib69tJjXoh/34oQX0zJYEQXhboy1+3eeNm5axvN3Tn7B6vwTC52fng5DfSvTbYE9bGKLWsLfaeZZbuvnl79DCr9Hi6vnK9+aBHKdzmi1lHCHZlcT7nMbvfMvurrrMuC1EN85k86ZAFeOcHcg3Jcj/bXwnMzl2nasBOHuQLgvx4DXwnmNKcftWAvC3YFwX46Br4V1HpZgx5oQ7rnorg7AwhHuueiuDsDCEe656K4OwMIR7rnorg7AwhHuueiuDsDCEe656K4OwMIR7rnorg7AwhHuueiuDsDCaQx399d/h7++ajqEO4CC9IW7cBOJ7t+i7w7ysyZGuAMoSF24O7Nd+hapnOlOuAMoSFu4S5ktfxV83A3fhiPcARSkLNzF43HHQXrmY3fCHUBBusLdOhq3v/m1f7OlbOlOuAMoSFe4W3HtDfe8EzOEO4CCVIW7I62d8y9ZD90JdwAFEe6EOwCFCPdc8zKEO4CCCHeO3AEoRLgT7gAUUhXujrR2hTtXywBQS1e4e/4WVQh3rnMHoJaucJfTnb9QBbA6ysI94Wic75YBoJi2cI8+Hs+d7YQ7gJLUhXtkuvN97gBU0xfuUbdZ4k5MAHTTGO7LoLs6AAtHuOeiuzoAC0e456K7OgALVzjcAQBZlA33gkvPTXd1Ray8pSsv39CBRIR7LrqrK2LlLV15+YYOJCLcc9FdXRHZWlrN/m/QWq5+i6IDSQj3XHRXV8RELZ0/yqeJe7YoOpCEcM9Fd3VFDG1p8eCeJujZouhAEsI9F93VFZHe0uIxPWW+s0XRgSSEey7XUl39DWon/q9k6D634/Q9PfJTxK/Yj1zoxeTh/rrvrOXB+2R37dX+tTKmMq+V+BRh2NMzvUscX35YiVe/vnVx7zej5OiAYoR7LtdQnbgvena3iN27s+eKu3fqQi/SW5oc1k1MDwv3g/zTXoK331GKhnuBVz/urd9p6g4oR7jncgXVNbviZd9qHkg6mqr31/OvBL9Qf8RC01vqjs5TEJ/j9bQa1Wv85El9AH7+lUNdh+9XTrU2bxUlw73Eq/+633R+3IR97CKvYJ9aEsI9l8VX19sva/UOnrB/978XP7B7j1rohOFeh0rvOL0ON8/Be+9ffQy+O3TeMHzh/lptTuOXDvcir76gXmTksfvi96llIdxzWXx18o6YtLMJTw/s3qMWOmG476SD9NNqxIb7rnvsH3Pk3nt3KRfuRV796PVwWPw+tSyEey5Lr048dEu8Q5Uwhj3ras+3D13oZOHem05xHYlHHLZ3otyec98tNdyLvPrOMfKdUV81wj2XpVfn2K0ce71IOs7znzIbt9CJw91KXiGv4w/bTcrVMgsJ95lffcdaxB/pL32fWhjCPZelVzd+9476DH86lqufpibcD4ED8/YbgPi0qw/3Aa/+8IU1lr5PLQzhnsvSqxv7wTx612w/Ucu0jHg+Nn5BSwn3mV/9jsTpfWPM8vephSHcc1l8dZ5TahE7bcK+2R5y1EInC3fvCdVwZMcdtnsWVD7cy7z6J4lXQJ4tfp9aFsI9l8VX57kYLrjXNntn1N7dORocs9CZLoX0/53q+Xejzrs65n8WEO5FXv32bycnu7mCfWpZCPdcll/d6ezXec9zPGDvht7P2p19PnYZUVExYbif/0z00E3bSxC7ZlTcMy27XuKfzq+KbwOlw73Mq5/0vmBb/j61KIR7LtdQnfjX4v3Llu1d0X2AJ//5efepoYW6TRju5+P0nt5F63b+eq6Fd9Qe8Rz5z2LHl+9X4NV3PCP2OH7qDihHuOdyJdV1L14T50blCVNXHPeuhhP3Wu9C3dJbGjXBIieseIQe+sKv3pWA/el7x7WShcLdzP/qE+5zItxz0V1dEZOH+7L/jS9fGzqQhHDPRXd1RUzd0uLxTbinoQNJCPdcdFdXBOE+afnXhw4kIdxz0V1dEWsK9xnKvz50IAnhnovu6opYUrhPNY4vzTOXf33oQBLCPRfd1RWxmHCfeczT0KvfouhAEsI9F93VFVE03MuPzxZFB5IQ7rk4LugFgFmUjb+CS89Nd3UAFo5wz0V3dQAWjnDPRXd1ABaOcM9Fd3UAFo5wz0V3dbh2abemxhUi3HPRXV05hNIkaKN+hHsuadX1vwuVvc6ln0rpt1m+bv6vS+7+1L0VeW+QPWTw3nf9OkbAnAj3XKKrk3cL8t1hzeEufR26dZejmHh93W8c99gbOjjhvjyEey6R1Z12qW6UWzcsw8l65xMcd0Zy/rh5QAhYIdvHDr7el2W5CPdcoqobd0vJVVprigTq9tzw2kr3w67/6PjB1/qyLBnhnktMdZF3mzfWp17pvpab/evlo3XzBNfjraW7PkC3l9j54WnMzu9LNUSuc3sc6WN8e5jdwU6Rw846pAwNK84heCegh3Ug0JH2L3pfKSNPpPS76Yjx/lCObB83OOG+PIR7LhHVRU4XOybl+zm92WysH7oeD8Wb9ePWSlpjSmk0ZJ2tJRn3TTcD4e4bNmLIKTpg8S/X+Up1q3Sd8XRsSlLkCkk9weCE+/IQ7rlEVBd14H7a41pPax7qxU0l7ICOx+3ZoO7+2zuSe91vvMuy1idpnftvOPZZOnvgQLj7hu013RdcIzpgCyzX9Qr2C3e8N3ivfrE+dvSWMsXgCWdzMRPCPZeI6mLCXQ4fMRqEXUl+XPwU3n6q91RAL0xb69ON0wHr3EsRcZyYaRnPsHbtUj1jO2ALLdf1CnbXR5pW2+xfE8Ldve7jBifcl4dwzyWiupiPso6dvverYkA5H3dNEFgXP4h7qDhmZzUHr7P0DPk9IhDu7mH7ceecGhvVAVtoua5X0Lual6OD2GkZzzvZuMGZllkewj2XmOoiDt0LhXt7Kb0fXHe4i9WHj5gTOyDxLzcQ7sFeeM559t9R7KVMMDjhvjyEey5R1TmuVWuRd5rY4z758dDFEeJKet9Iuk8ZvM6TTcsEjtx9Zy4n6YAttNxQuEu9aD/muVqx109hIRMMTrgvD+GeS1x10hlC07rYTjxXZ/91Slq4izPKr/tNe5HWac1utNkxLVxsk7zO/YQYfELVPWyrsx6jOyC+lQWP633ZaDWw1xxr4tzxgLiMrIOjEMI9l9jqnJcqnPc0eRYlfFLQ87h/TGmVhMtRPOszcJ3thLDHqY9+R865e9d9kg704z603GC4h9dcXK3+O6VjEWMHJ9wXiHDPJak6a9cRZ3TlGDn/OCXchYV2ntb9mf2j3aGTB77DwYR1FhOiNcxm/2r/XuKcu+vN1N/x5A5YMxmB5YbD3Vop/1ng/hPCc3EjBifcl4hwz0VtdXExtFDi1HjMJanW89M6MMlyx0g8zwIFCPdc1FZ3zeHuOUWbEHzpHZhmuSMEr+WBPoR7Lmqru+Zwd5/hSCloQAcmWe5wZPsaEe65qK3uqsPdmIgTHFEDpHdg9HKBFIR7LrqrA7BwhHsuuqvDQG9v5ng0x6P58cN8/26OR/P+XnqdoFPhcAc02VbV16r6XlXHqjpW1UtVmYh/P6vqc1XdlF55aFM23AsuPTfd1RUxQUt//26Omh8ehH8/fw4/lP7zx/zzTzjKt1uz3ZqvX5slfv5sPnxofnR7a3788CyBLYoOJCHcc9FdXRHJLX15Mb9+mYcH8+WL2W5jDqIv/z59Mp8/m4cHczya378DC3p6ajJ6u21+5eUlYT1//jR3d81y7+/N37/is9ii6EASwj0X3dUVkdDS5+fLEfH53+2tubvrH6c/P18e+frVbLfm0ydn4v/vf2a7bUL/8bGZPf/33+an37+PKu/3b/Pxo6kq8/nz2PKVogNJVhXu1aB/QxfGhji12JY+PFzmQL59a85bvr2lLez93RyP5vHRPDw0cyk3N87Q/+ef8NF9jLc3c3trqsocj/YP2aLoQBLd4T4szacJejbEyUW1tE72Dx/Mr19ZVqKetX96ambM6/cPx0TKEM/PpqrMx4/2mGxRdCAJ4Z4r8dkQJxdo6fu7+fy5SfY/f+ZaqQzqeZ77+97DbFF0IMmKw/21Ev8i/OB+pvCjEuHe/VN2/585uu99LP41uv1N5c4xnPd88I0/TqCldSbe3p6Tfe5GyWOlfr+iMW9vzeT742NC+eGqcncgYYRhm8qADqzZisP9IG+GvQR/3Tt/VCLcU+9DnLTHXv4+Xvpq8h73F/O6njKar6Xv702yN3PrJRrV/ZGjD3GNenkxNzfm5qb9EcRXfmxFWTsQOcLwTSWxA2u39nDf7H3POd2fpqq32vLhbt3xx77BUZjvfseb/d76jqmIb52y70SUg6+lP3+aqjJfv7pWaI5GRfQhoVHfv5uqMg8P5wfStqhCHQiOMGZTIdyTEO6BeZv9a2XMQsLdcyvLhF3Wd4fT3UGI8mC4z3WjBl9Lv341VWWenlorNHujgn1IatSfP6aqzN3d+YGULapQB4IjjNtUCPckhLv3Oad/ywh3z03o4/cX8eneO92H9uHZ7gPha2n9N0r//WeMKdWoYB/SGvX3b3Nl/UnKFlVoUwmNMHJTIdyTrD3cO3bLDnffZ+TYPVYeo/0dto5w7zbKupt3tTvkPp3qaenfv+bmxnz82PxvoUYF+5DcqPqayMv/RW9RpTaV0AgjNxXCPcmKwz3+aplFhbu1a6bc0Md9t7fzY67ZBmfAu0+jzXZC9eWlM4NRplHBPqQ3amS4z7+pBEYYu6lMv0+ptuJwd5w+FY/flYS7tMP299DYz9pWZrWHHXLyLszZ0vps6pcvzf+WaVSwD+mNKhju4zcVYYSxmwrhnoRwt47lN9XrksN9+Gdt6fftSdCYO7J1RvJ8fJ/42N3Z0qenzleylGlUsA/pjSo2LTN+U0m4a2z8pkK4JyHcrYP3xYa77yxZxIGPtA95rkz2DtpZprgCOa6gcba0/pP9y/dtlWlUsA/JjRoc7sU3FUdgj9xUCPckhLt15L7YaRnf9W3BXaPZN8VLH5LDvbs7Og/zZpuWqefct1vv0rM3KtiHtEa9vY24WqbspiKP4FithE2FcE+y3nDfVdXuYCV778Flhbs9Z+l4wN5T4vcgaWI1MHFqTZs2T5n6ihlfSz98MB8+uNdxhkZF9CGpUcfjiOvcC3UgOMK4TYVwT7LqcBfsIp7Tn7eZszrxqwBa2ev4+7+EGXDxrJl3mel/6T6Qr6X1l7A317m7Vjtro0xEH1Ia9eOHqSrz7VtU+a71m7sDwRFGbSqJHVi79Yb7+Xj8rP5jVPtY3toUC4a76e8eMaesnJ+SJeHMknfFTpbk+ZMmX0vv762vQZ+/UeeHfX2IbVTnb26NGbJFlehAxAiDNxXCPYnucBeWmeGfY0lsiFPztfTbt95x7tWr78h6+SzCFkUH0hDuhPvV8LW0nsRof3dYccdj5+7bz8/meIy9rcfjY+9sqmGLogOJ1hbuhnC/Xr6W/vrVhHtVmX//nXGlLC8v5u5OuINr1boR69ev5vnZvL/LIzw9Nd/32711H1sUHUiywnBvFp412Q0bYga+lr6/N/c4rf/75cuUt76L9/R0ifV//22O2R8fm3ux3t83d+E4/7u7u9xou757X31m+ObGPD/3xmaLogNJVhvuPVPGejPigqpTItDS+gzk/X0Tr7e3Zrs1P37MsWbHo/nypcnleurf89by9maen83nz829sMVDe+l222xRdCAJ4Z6L7uqKCLT0/d18/25eXszLS3Mz1XNW1kfQx2P7/OQEfv26vJfU/25vxVx2+v3bfP9utluz3TZH+tYB+xlbFB1IQrjnoru6IpJb+udPc2PV3r9Pn8x2a758aUL/6ekyMeLy33+X5xyP5vn5cpxe/3FsPbuScy6ILYoOJCkc7kBun6pqW1X/V1WPVXWsqnfXec70fy9VdVdVN6ULBGRlw73g0nPTXV0Rk7X0719zPJqfPy/XKd7fN3MjMf/u7/3zJ5mwRdGBJIR7LrqrK2LlLV15+YYOJCLcc9FdXRErb+nKyzd0IBHhnovu6opYeUtXXr6hA4kI91x0V1fEylu68vINHUhEuOeiu7oiVt7SlZdv6ECiFYe7fGsZ6XbvJ0lfZLuQDbFbpf+rXD032/F9d63YFu+3zSat1UVqS+etPXaEYbWbQVtUiVc//AXRc3ZgzVYc7vJdKC6bWlT4uy1gQ0y9MULS7n1pn3yrzrS+Tn6XtflrjxlhzltVFHn1QzsVN+uY0drDPbCxC3fRuZ4N0brVjnWPswiOW6a97jdVtdnvhR467vAzwVoltLRQ7YERxq1V2hZVogP2jTr6azFnB1aPcE/Y1BPuQFa8Ot8tkhOKlu9Mf37U7mHgVvaj1iq6pYVqD4wwdq1StqgyHZBacthdhpizAyDck8P9Wo7c5ZVNen9yPL21y1sLaY7pnC0atVbRLS1Te2iEsWuVskUVfPWFm4afHpmzA1h9uHcEtq/AQWlP4ep8H6hja5DHaB+Kycduu4PrdOq4tYptaaHaAyOMXquELapYB04vfP2MXmzP2QGsOtwTT5g6tkynRVRnVZNShXhE1d657d3bfVKu/pVxa5UW7nPXHhph9Folh3uhDrSPmjq/P2cHsOpw7zttk2K8p0Z78erG797S3t3fnV3h3v6t9imzawn3IbWHRriucB/cAev9vf/ZhXCfC+He4tzKEucqjTHFqxv7EVj6fXtCXQ538aN8tTtcy7TMsNqjRriSaZmhHbB2lM7VMUzLzItwb5P218QrIM9KV+c5eRVRi/R25rkQ+jyo52DOcxYycq2iW1qmdv8IY9dqshOq+TrgefE9W0emDoBwb7MPIYYmuylfneeys+BBkn29cutRb8CFDlnHrNUkl0JmrN0/wsjazWSXQmbrgOPAvJXdc3YA6w33w0482yP8KWXabMxZ8Q3RKsjxgP3OFT8J6vpgbk20nh8Ir5VbfEvL1B4aYUztJnGLKtEB6Q+Sun+1NGcHsOpwF9jThfJRStgCNkSxAs+fD3YejtrdPBfDOVsWWiu3lJYWqT04wvDaTfIWVaADrqN7+w1glg6s3WrD3Vibojxx6t9UPUpXV3NdcN76oXyOIW5/i7gYzn1wm9ZPM/LLVeapPTzCwNrNkC2qRAf6u43ro8E8HVi1NYd7XrqrK2LlLV15+YYOJCLcc9FdXRErb+nKyzd0IBHhnovu6opYeUtXXr6hA4kI91x0V1fEylu68vINHUhEuOeiu7oiVt7SlZdv6EAiwj0X3dUVsfKWrrx8QwcSEe656K6uiJW3dOXlGzqQqHC4AwCyKBjuAIBMCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCF/h/5RydN136RwQAAAABJRU5ErkJggg==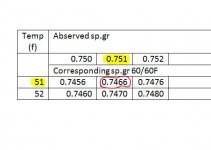
من مدتی هست که در آزمایشگاه مرکزی پالایشگاه آبادان مشغول به کار شدم و کارم تعییین چگالی نسبی مواد نفتی هست. متاسفانه با توجه به قدیمی بودن وسایل ما برای تعیین sp.gr محصولات نفتی مثل kerosin , gasoil, ord, mco, و... ابتدا دمای این مایعات رو با ترمومتر اندازه میگیریم سپس با هیدرومتر مناسب sp.gr رو هم یادداشت میکنیم.
سپس با استفاده از جدول23 از astm d1298 یا astm d1250 گراویتی مورد نظر در 60 درجه فارنهایت رو پیدا کرده و یادداشت میکنیم.
مدتی ایست که در پی فرمولی برای محاسبه و کانورت گراویتی هستم که بتوان با دادن دامی محصول و گراویتیش در همان دما (مثلا 70درجه فارنهایت) بتوان گراویتی در 60 درجه فارنهایت رو بدست بیارم.
مطالب زیادی خوندم و فرمولهای زیادی رو از سایتهای خارجی امتحان کردم ولی جواب درستی حاصل نشده چون منحنی تغییرات غیرخطی ایست.
امیدوارم مهندسین ایرانی عزیز بتونید به من کمک کنید.
یرای درستی و صحت کارتون من از روی قسمتی از جدول رو میگذارم تا محاسباتتون دقیق بشه
طبق جدول بالا در دمای 51 درجه گراویتی محصول که با هیدرومتر مشاهده شده 0.751 بوده که طبق جدول گراویتی آن در 60 فارانهایت 0.7466 میباشد.
دوستاان لطف کنید جوابتون رو به ایمیلم ob_z2006@yahoo.com یا با شماره 09374411865 بلواری زاده پیامک کنید.منتظر کمکتون هستمhttp://www.www.www.iran-eng.ir/image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAfQAAAFlCAIAAACSjo07AAAbl0lEQVR4nO3dL3DbytfGccHAwsDCC3+wY2R4YWBgkaewsCwvK4xZYWBgmQsNCwsDAi4MDCzcF0i2Je3Zf5JWKx99P9O5M9dxVjrH0mN5pViVAQCoU5VeAQDA9Ah3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCIcAcAhQh3AFCoZLhXAIBMyoZ7waXnprs6AAtHuOeiuzoAC0e456K7OgALR7jnors6AAtHuOeiuzoAC0e45zJldYddVVW7w2TjlfO632gpBVi2JYd7HQROm/3rTCs6SGK4n4oVc49wB5CIcM8lLdwPu1NZUvAR7gASLTncO64uFZKqq9N776qRcAeQiHDPJaW6U3i7iiTcASRSEu6XWQ17vuawqx9qz/I04wgP9X+rM3RKKCVU18puOcbPj3pXpl2NPWcV06Lzc5xvNPUzWo/6hu2vlOfty7v+g18LcWLv0uh+yYAmCsLdswcbY5rdeGM9Z7fb9R6xA8X+rfgMiK/unF2n/7FC8tBfVXtlrC60x0hu0e4gd7y7dqFhY9Y7Zv2HvRb+hYslA4pcfbg3oWDF3CUbrGOz1l7ffaidh6cnXR5rlhR7Hje6uk62N4sRjqz9K9P7rdf9xnpuRIu6i7Vb3sn24LBWw84B7ngZHes/7LXofcaIKxnQ49rDXYrC3vGlfSzc39Gl4aX5kaQJ48jqXveb3pBCSeGVsZPWN164Ra1Be4HYyXbfsEKXU96jk8qPqbo7iqNkQI1rD3fXZ+9+cgmzC3aihsI9KRHiqnNe7unJJXllWiMJ7wzJLWqNeXqa8IbgG1ZsVtTsmviWkfha9N9axDcqpmKgGOHuGH6ecPdcym/NEUWtzGXA+BT2JV1rIb0nTR3uzvUf+loIKxgaE1Dk2sNdnBzomi7crUtFfGKqc619f0Gp8xKd3x/Wos6PzpeV9CfYfcMmTct41n/Ya1GvnvuMKeEO7a493MXJ2tf9xv8BPDbcK+uDfHwgRFTnTjop3aTj5vaUe/+krHc+Ptii7qps9ntHyzzDJpxQ9a5/1GshTbsEj+sJdyh29eHumh+YKtzdH+xHV+c7+Oz+zHEtoDjhLh2pDmhRf1WkVQ0NKzyhrsJ7ib69tJjXoh/34oQX0zJYEQXhboy1+3eeNm5axvN3Tn7B6vwTC52fng5DfSvTbYE9bGKLWsLfaeZZbuvnl79DCr9Hi6vnK9+aBHKdzmi1lHCHZlcT7nMbvfMvurrrMuC1EN85k86ZAFeOcHcg3Jcj/bXwnMzl2nasBOHuQLgvx4DXwnmNKcftWAvC3YFwX46Br4V1HpZgx5oQ7rnorg7AwhHuueiuDsDCEe656K4OwMIR7rnorg7AwhHuueiuDsDCEe656K4OwMIR7rnorg7AwhHuueiuDsDCaQx399d/h7++ajqEO4CC9IW7cBOJ7t+i7w7ysyZGuAMoSF24O7Nd+hapnOlOuAMoSFu4S5ktfxV83A3fhiPcARSkLNzF43HHQXrmY3fCHUBBusLdOhq3v/m1f7OlbOlOuAMoSFe4W3HtDfe8EzOEO4CCVIW7I62d8y9ZD90JdwAFEe6EOwCFCPdc8zKEO4CCCHeO3AEoRLgT7gAUUhXujrR2hTtXywBQS1e4e/4WVQh3rnMHoJaucJfTnb9QBbA6ysI94Wic75YBoJi2cI8+Hs+d7YQ7gJLUhXtkuvN97gBU0xfuUbdZ4k5MAHTTGO7LoLs6AAtHuOeiuzoAC0e456K7OgALVzjcAQBZlA33gkvPTXd1Ray8pSsv39CBRIR7LrqrK2LlLV15+YYOJCLcc9FdXRHZWlrN/m/QWq5+i6IDSQj3XHRXV8RELZ0/yqeJe7YoOpCEcM9Fd3VFDG1p8eCeJujZouhAEsI9F93VFZHe0uIxPWW+s0XRgSSEey7XUl39DWon/q9k6D634/Q9PfJTxK/Yj1zoxeTh/rrvrOXB+2R37dX+tTKmMq+V+BRh2NMzvUscX35YiVe/vnVx7zej5OiAYoR7LtdQnbgvena3iN27s+eKu3fqQi/SW5oc1k1MDwv3g/zTXoK331GKhnuBVz/urd9p6g4oR7jncgXVNbviZd9qHkg6mqr31/OvBL9Qf8RC01vqjs5TEJ/j9bQa1Wv85El9AH7+lUNdh+9XTrU2bxUlw73Eq/+633R+3IR97CKvYJ9aEsI9l8VX19sva/UOnrB/978XP7B7j1rohOFeh0rvOL0ON8/Be+9ffQy+O3TeMHzh/lptTuOXDvcir76gXmTksfvi96llIdxzWXx18o6YtLMJTw/s3qMWOmG476SD9NNqxIb7rnvsH3Pk3nt3KRfuRV796PVwWPw+tSyEey5Lr048dEu8Q5Uwhj3ras+3D13oZOHem05xHYlHHLZ3otyec98tNdyLvPrOMfKdUV81wj2XpVfn2K0ce71IOs7znzIbt9CJw91KXiGv4w/bTcrVMgsJ95lffcdaxB/pL32fWhjCPZelVzd+9476DH86lqufpibcD4ED8/YbgPi0qw/3Aa/+8IU1lr5PLQzhnsvSqxv7wTx612w/Ucu0jHg+Nn5BSwn3mV/9jsTpfWPM8vephSHcc1l8dZ5TahE7bcK+2R5y1EInC3fvCdVwZMcdtnsWVD7cy7z6J4lXQJ4tfp9aFsI9l8VX57kYLrjXNntn1N7dORocs9CZLoX0/53q+Xejzrs65n8WEO5FXv32bycnu7mCfWpZCPdcll/d6ezXec9zPGDvht7P2p19PnYZUVExYbif/0z00E3bSxC7ZlTcMy27XuKfzq+KbwOlw73Mq5/0vmBb/j61KIR7LtdQnfjX4v3Llu1d0X2AJ//5efepoYW6TRju5+P0nt5F63b+eq6Fd9Qe8Rz5z2LHl+9X4NV3PCP2OH7qDihHuOdyJdV1L14T50blCVNXHPeuhhP3Wu9C3dJbGjXBIieseIQe+sKv3pWA/el7x7WShcLdzP/qE+5zItxz0V1dEZOH+7L/jS9fGzqQhHDPRXd1RUzd0uLxTbinoQNJCPdcdFdXBOE+afnXhw4kIdxz0V1dEWsK9xnKvz50IAnhnovu6opYUrhPNY4vzTOXf33oQBLCPRfd1RWxmHCfeczT0KvfouhAEsI9F93VFVE03MuPzxZFB5IQ7rk4LugFgFmUjb+CS89Nd3UAFo5wz0V3dQAWjnDPRXd1ABaOcM9Fd3UAFo5wz0V3dbh2abemxhUi3HPRXV05hNIkaKN+hHsuadX1vwuVvc6ln0rpt1m+bv6vS+7+1L0VeW+QPWTw3nf9OkbAnAj3XKKrk3cL8t1hzeEufR26dZejmHh93W8c99gbOjjhvjyEey6R1Z12qW6UWzcsw8l65xMcd0Zy/rh5QAhYIdvHDr7el2W5CPdcoqobd0vJVVprigTq9tzw2kr3w67/6PjB1/qyLBnhnktMdZF3mzfWp17pvpab/evlo3XzBNfjraW7PkC3l9j54WnMzu9LNUSuc3sc6WN8e5jdwU6Rw846pAwNK84heCegh3Ug0JH2L3pfKSNPpPS76Yjx/lCObB83OOG+PIR7LhHVRU4XOybl+zm92WysH7oeD8Wb9ePWSlpjSmk0ZJ2tJRn3TTcD4e4bNmLIKTpg8S/X+Up1q3Sd8XRsSlLkCkk9weCE+/IQ7rlEVBd14H7a41pPax7qxU0l7ICOx+3ZoO7+2zuSe91vvMuy1idpnftvOPZZOnvgQLj7hu013RdcIzpgCyzX9Qr2C3e8N3ivfrE+dvSWMsXgCWdzMRPCPZeI6mLCXQ4fMRqEXUl+XPwU3n6q91RAL0xb69ON0wHr3EsRcZyYaRnPsHbtUj1jO2ALLdf1CnbXR5pW2+xfE8Ldve7jBifcl4dwzyWiupiPso6dvverYkA5H3dNEFgXP4h7qDhmZzUHr7P0DPk9IhDu7mH7ceecGhvVAVtoua5X0Lual6OD2GkZzzvZuMGZllkewj2XmOoiDt0LhXt7Kb0fXHe4i9WHj5gTOyDxLzcQ7sFeeM559t9R7KVMMDjhvjyEey5R1TmuVWuRd5rY4z758dDFEeJKet9Iuk8ZvM6TTcsEjtx9Zy4n6YAttNxQuEu9aD/muVqx109hIRMMTrgvD+GeS1x10hlC07rYTjxXZ/91Slq4izPKr/tNe5HWac1utNkxLVxsk7zO/YQYfELVPWyrsx6jOyC+lQWP633ZaDWw1xxr4tzxgLiMrIOjEMI9l9jqnJcqnPc0eRYlfFLQ87h/TGmVhMtRPOszcJ3thLDHqY9+R865e9d9kg704z603GC4h9dcXK3+O6VjEWMHJ9wXiHDPJak6a9cRZ3TlGDn/OCXchYV2ntb9mf2j3aGTB77DwYR1FhOiNcxm/2r/XuKcu+vN1N/x5A5YMxmB5YbD3Vop/1ng/hPCc3EjBifcl4hwz0VtdXExtFDi1HjMJanW89M6MMlyx0g8zwIFCPdc1FZ3zeHuOUWbEHzpHZhmuSMEr+WBPoR7Lmqru+Zwd5/hSCloQAcmWe5wZPsaEe65qK3uqsPdmIgTHFEDpHdg9HKBFIR7LrqrA7BwhHsuuqvDQG9v5ng0x6P58cN8/26OR/P+XnqdoFPhcAc02VbV16r6XlXHqjpW1UtVmYh/P6vqc1XdlF55aFM23AsuPTfd1RUxQUt//26Omh8ehH8/fw4/lP7zx/zzTzjKt1uz3ZqvX5slfv5sPnxofnR7a3788CyBLYoOJCHcc9FdXRHJLX15Mb9+mYcH8+WL2W5jDqIv/z59Mp8/m4cHczya378DC3p6ajJ6u21+5eUlYT1//jR3d81y7+/N37/is9ii6EASwj0X3dUVkdDS5+fLEfH53+2tubvrH6c/P18e+frVbLfm0ydn4v/vf2a7bUL/8bGZPf/33+an37+PKu/3b/Pxo6kq8/nz2PKVogNJVhXu1aB/QxfGhji12JY+PFzmQL59a85bvr2lLez93RyP5vHRPDw0cyk3N87Q/+ef8NF9jLc3c3trqsocj/YP2aLoQBLd4T4szacJejbEyUW1tE72Dx/Mr19ZVqKetX96ambM6/cPx0TKEM/PpqrMx4/2mGxRdCAJ4Z4r8dkQJxdo6fu7+fy5SfY/f+ZaqQzqeZ77+97DbFF0IMmKw/21Ev8i/OB+pvCjEuHe/VN2/585uu99LP41uv1N5c4xnPd88I0/TqCldSbe3p6Tfe5GyWOlfr+iMW9vzeT742NC+eGqcncgYYRhm8qADqzZisP9IG+GvQR/3Tt/VCLcU+9DnLTHXv4+Xvpq8h73F/O6njKar6Xv702yN3PrJRrV/ZGjD3GNenkxNzfm5qb9EcRXfmxFWTsQOcLwTSWxA2u39nDf7H3POd2fpqq32vLhbt3xx77BUZjvfseb/d76jqmIb52y70SUg6+lP3+aqjJfv7pWaI5GRfQhoVHfv5uqMg8P5wfStqhCHQiOMGZTIdyTEO6BeZv9a2XMQsLdcyvLhF3Wd4fT3UGI8mC4z3WjBl9Lv341VWWenlorNHujgn1IatSfP6aqzN3d+YGULapQB4IjjNtUCPckhLv3Oad/ywh3z03o4/cX8eneO92H9uHZ7gPha2n9N0r//WeMKdWoYB/SGvX3b3Nl/UnKFlVoUwmNMHJTIdyTrD3cO3bLDnffZ+TYPVYeo/0dto5w7zbKupt3tTvkPp3qaenfv+bmxnz82PxvoUYF+5DcqPqayMv/RW9RpTaV0AgjNxXCPcmKwz3+aplFhbu1a6bc0Md9t7fzY67ZBmfAu0+jzXZC9eWlM4NRplHBPqQ3amS4z7+pBEYYu6lMv0+ptuJwd5w+FY/flYS7tMP299DYz9pWZrWHHXLyLszZ0vps6pcvzf+WaVSwD+mNKhju4zcVYYSxmwrhnoRwt47lN9XrksN9+Gdt6fftSdCYO7J1RvJ8fJ/42N3Z0qenzleylGlUsA/pjSo2LTN+U0m4a2z8pkK4JyHcrYP3xYa77yxZxIGPtA95rkz2DtpZprgCOa6gcba0/pP9y/dtlWlUsA/JjRoc7sU3FUdgj9xUCPckhLt15L7YaRnf9W3BXaPZN8VLH5LDvbs7Og/zZpuWqefct1vv0rM3KtiHtEa9vY24WqbspiKP4FithE2FcE+y3nDfVdXuYCV778Flhbs9Z+l4wN5T4vcgaWI1MHFqTZs2T5n6ihlfSz98MB8+uNdxhkZF9CGpUcfjiOvcC3UgOMK4TYVwT7LqcBfsIp7Tn7eZszrxqwBa2ev4+7+EGXDxrJl3mel/6T6Qr6X1l7A317m7Vjtro0xEH1Ia9eOHqSrz7VtU+a71m7sDwRFGbSqJHVi79Yb7+Xj8rP5jVPtY3toUC4a76e8eMaesnJ+SJeHMknfFTpbk+ZMmX0vv762vQZ+/UeeHfX2IbVTnb26NGbJFlehAxAiDNxXCPYnucBeWmeGfY0lsiFPztfTbt95x7tWr78h6+SzCFkUH0hDuhPvV8LW0nsRof3dYccdj5+7bz8/meIy9rcfjY+9sqmGLogOJ1hbuhnC/Xr6W/vrVhHtVmX//nXGlLC8v5u5OuINr1boR69ev5vnZvL/LIzw9Nd/32711H1sUHUiywnBvFp412Q0bYga+lr6/N/c4rf/75cuUt76L9/R0ifV//22O2R8fm3ux3t83d+E4/7u7u9xou757X31m+ObGPD/3xmaLogNJVhvuPVPGejPigqpTItDS+gzk/X0Tr7e3Zrs1P37MsWbHo/nypcnleurf89by9maen83nz829sMVDe+l222xRdCAJ4Z6L7uqKCLT0/d18/25eXszLS3Mz1XNW1kfQx2P7/OQEfv26vJfU/25vxVx2+v3bfP9utluz3TZH+tYB+xlbFB1IQrjnoru6IpJb+udPc2PV3r9Pn8x2a758aUL/6ekyMeLy33+X5xyP5vn5cpxe/3FsPbuScy6ILYoOJCkc7kBun6pqW1X/V1WPVXWsqnfXec70fy9VdVdVN6ULBGRlw73g0nPTXV0Rk7X0719zPJqfPy/XKd7fN3MjMf/u7/3zJ5mwRdGBJIR7LrqrK2LlLV15+YYOJCLcc9FdXRErb+nKyzd0IBHhnovu6opYeUtXXr6hA4kI91x0V1fEylu68vINHUhEuOeiu7oiVt7SlZdv6ECiFYe7fGsZ6XbvJ0lfZLuQDbFbpf+rXD032/F9d63YFu+3zSat1UVqS+etPXaEYbWbQVtUiVc//AXRc3ZgzVYc7vJdKC6bWlT4uy1gQ0y9MULS7n1pn3yrzrS+Tn6XtflrjxlhzltVFHn1QzsVN+uY0drDPbCxC3fRuZ4N0brVjnWPswiOW6a97jdVtdnvhR467vAzwVoltLRQ7YERxq1V2hZVogP2jTr6azFnB1aPcE/Y1BPuQFa8Ot8tkhOKlu9Mf37U7mHgVvaj1iq6pYVqD4wwdq1StqgyHZBacthdhpizAyDck8P9Wo7c5ZVNen9yPL21y1sLaY7pnC0atVbRLS1Te2iEsWuVskUVfPWFm4afHpmzA1h9uHcEtq/AQWlP4ep8H6hja5DHaB+Kycduu4PrdOq4tYptaaHaAyOMXquELapYB04vfP2MXmzP2QGsOtwTT5g6tkynRVRnVZNShXhE1d657d3bfVKu/pVxa5UW7nPXHhph9Folh3uhDrSPmjq/P2cHsOpw7zttk2K8p0Z78erG797S3t3fnV3h3v6t9imzawn3IbWHRriucB/cAev9vf/ZhXCfC+He4tzKEucqjTHFqxv7EVj6fXtCXQ538aN8tTtcy7TMsNqjRriSaZmhHbB2lM7VMUzLzItwb5P218QrIM9KV+c5eRVRi/R25rkQ+jyo52DOcxYycq2iW1qmdv8IY9dqshOq+TrgefE9W0emDoBwb7MPIYYmuylfneeys+BBkn29cutRb8CFDlnHrNUkl0JmrN0/wsjazWSXQmbrgOPAvJXdc3YA6w33w0482yP8KWXabMxZ8Q3RKsjxgP3OFT8J6vpgbk20nh8Ir5VbfEvL1B4aYUztJnGLKtEB6Q+Sun+1NGcHsOpwF9jThfJRStgCNkSxAs+fD3YejtrdPBfDOVsWWiu3lJYWqT04wvDaTfIWVaADrqN7+w1glg6s3WrD3Vibojxx6t9UPUpXV3NdcN76oXyOIW5/i7gYzn1wm9ZPM/LLVeapPTzCwNrNkC2qRAf6u43ro8E8HVi1NYd7XrqrK2LlLV15+YYOJCLcc9FdXRErb+nKyzd0IBHhnovu6opYeUtXXr6hA4kI91x0V1fEylu68vINHUhEuOeiu7oiVt7SlZdv6EAiwj0X3dUVsfKWrrx8QwcSEe656K6uiJW3dOXlGzqQqHC4AwCyKBjuAIBMCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCFCHcAUIhwBwCF/h/5RydN136RwQAAAABJRU5ErkJggg==

